Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 6.Problemas propostos - Ex. 67
Obter uma equação geral do plano que contenha o ponto e a reta dados:
e a reta interseção do plano com o plano
Passo 1
Vamos primeiro lembrar quem é esse plano , é exatamente esse plano aqui:
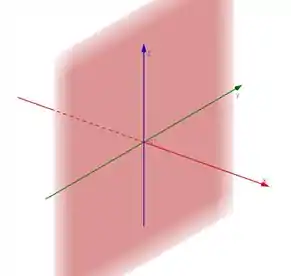
Que, podemos perceber na figura que é onde
Então temos que a reta interseção é dada desse sisteminha:
Passo 2
Vamos resolver esse sisteminha então para achar a equação dela:
Como ,
Então, chamando o y de , ficamos com a equação vetorial:
Passo 3
Para acharmos a equação do plano precisamos de 3 pontos, o primeiro o enunciado nos diz que é o ponto , para achar os outros dois pontos vamos atribuir dois valores qualquer para , por exemplo e :
Para , temos:
Para , temos:
Passo 4
Agora que temos nossos 3 pontos, vamos achar com eles, dois vetores que chamaremos de e
Passo 5
Colocando o ponto e os vetores e na matriz, temos:
Achando o determinante dessa matriz, ficamos com:
Que podemos escrever como