Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 8.Exercícios Propostos - Ex. 28

Sejam S :   x 2 + y 2   + z 2   - 8 x   - 10 y   - 8 z   +   30   =   0 e

S ' :   x 2   + y 2   +   z 2     + 2 x   + 2 z   = 10 . Ache a superfície esférica S ' ' , de maior raio, que seja tangente a S e S ' e tal que os centros de S , S ' e S ' ' pertençam a uma mesma reta.

Passo 1

Tudo tranquilo? Vamos escrever as equações das superfícies esféricas na forma reduzida:

x 2 + y 2   + z 2   - 8 x   - 10 y   - 8 z   +   30   =   0 :

⇒   x 2 - 8 x + 16 - 16   + y 2 - 10 y + 25 - 25 + z 2 - 8 z   + 16 - 16 +   30   =   0  

⇒   ( x   - 4 ) 2 + ( y   - 5 ) 2 + ( z   - 4 ) 2 = 27

cujo centro é C   =   ( 4,5 , 4 )   e o raio r   = 27

x 2   + y 2   +   z 2     + 2 x   + 2 z   = 10 :

⇒ x 2   + 2 x   + 1 - 1 + y 2 + z 2   + 2 z   +   1 - 1 = 10

⇒   ( x   + 1 ) 2   + y 2 + ( z   + 1 ) 2   = 12

nos informando que C '   =   ( - 1,0 , - 1 )   e r '   =   12

Passo 2

Agora, vamos verificar a distância entre os dois centros:

d ( C , C ' )   =   ( x '   - x ) 2   +   ( y '   - y ) 2   +   ( z '   - z ) 2

⇒ d ( C , C ' )   =   ( - 1 - 4 ) 2   +   ( 0   - 5 ) 2   +   ( - 1 - 4 ) 2  

⇒ d ( C , C ' )   =   25   +   25 + 25 = 75     ≈ 8,66

Como os centros estão na mesma reta e queremos a esfera de maior raio possível que seja tangente às outras duas:

2 r ' ' = d ( C , C ' )   + r   + r '  

⇒   2 r ' ' = 8,66 + 5,2   +   3,46

⇒   r ' ' = 17,32 2   = 8,66 ⇒ r ' 2 ' = 75

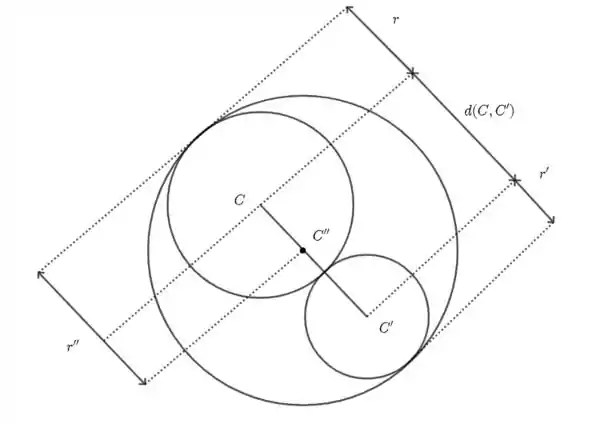
Precisamos construir uma superfície esférica S ' ' que os centros de S , S ' e S ' ' pertençam a uma mesma reta. Então,

S ' ' :   ( x - a ' ' ) 2   +   ( y - b ' ' ) 2   +   ( z - c ' ' ) 2   =   75

Passo 3

Temos dois centros conhecidos C   =   ( 4,5 , 4 ) e C '   =   ( - 1,0 , - 1 ) . O centro da esfera S ' ' passa pela mesma reta que os centros das outras esferas. Vamos calcular essa reta, cujo vetor diretor será paralelo a

C C ' → =   C '   -   C   =   ( - 1,0 , - 1 )   - ( 4,5 , 4 )   =   ( - 5 , - 5 ,   - 5 )    

Temos que um ponto da reta saindo de C na direção de C C ' → será da forma

P '   =   ( 4,5 , 4 ) + m ( - 5 , - 5 ,   - 5 ) =   ( 4 - 5 m ,   5 - 5 m ,   4 - 5 m )

Então C ' ' será da forma C ' '   =   ( 4 - 5 m ,   5 - 5 m ,   4 - 5 m ) para algum m valor de m. Daí, podemos calcular o vetor saindo de C até C ' ' :

C C ' ' → =   C ' '   -   C   =     ( 4 - 5 m ,   5 - 5 m ,   4 - 5 m ) - ( 4,5 , 4 )   =   ( - 5 m ,   - 5 m ,   - 5 m )    

O módulo desse vetor tem que ser igual a diferença entre o raio da esfera S ' ' e da esfera S :

| C C ' ' | →   = r ' ' - r = 8,66 - 5,2 = 3,46 ⇒ 75 m 2     = 3,46   ⇒ m   =   3,46 8,66   ≈ 0,4 = 2 5  

O ponto de intercessão vai ser

C ' '   =   ( 4 - 5 ⋅ 2 5 ,   5 - 5 ⋅ 2 5 ,   4 - 5 ⋅ 2 5 ) = ( 2,3 , 2 )

Portanto,

( x - 2 ) 2   +   ( y - 3 ) 2   +   ( z - 2 ) 2   =   75

Essa foi difícil, hein? Mas conseguimos chegar ao final do capítulo!

Resposta

( x - 2 ) 2   +   ( y - 3 ) 2   +   ( z - 2 ) 2   =   75

Exercícios de Livros Relacionados

Determine o centro e o raio da circunferência, interseção do plano 2 x- y+ 3 z-3=0 com a superfície x 2+y 2+ z 2- 2 y- 2 z- 2=0 .
Determine as coordenadas das extremidades do diâmetro da superfície esférica e que é paralelo a reta x+ 1 =- y +5=z -7 .
Ache os planos que passam pela reta t : ( x , y , z )=( 4,5 , - 2 )+m ( 1 , - 1,0 ) e que cortam sobre a superfície esférica S :( x - 1 ) 2+( y - 2 ) 2+ ( z - 1 ) 2 = 16 circunferências de raio 7 .
Dada a superfície esférica x 2 + y 2 + z 2 - 3 x - 9= 0 e o plano x+ y + z - 1 = 0 ,determine a posição relativa da superfície e o plano;se o plano for:externo, calcule a distância do centro ao plano;
Ache o centro e o raio da circunferência x^2 + y^2 + z^2 - 2 x + 4 y - 4 = 0 ⎨ x - 2 y + z + 1 = 0⎨