Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 3c

(c) Suponha que o quadrilátero ABCD do item anterior seja um paralelogramo. Mostre que as quatro diagonais (as duas de ABCD e as duas de MNPQ) têm um ponto comum.

Passo 1

Bora lá!

Esse é o nosso quadrilátero ACBD (eventualmente reverso), onde M divide (A,B), N divide (C,B), P divide (C,D) e Q divide (A,D), todos na razão r:

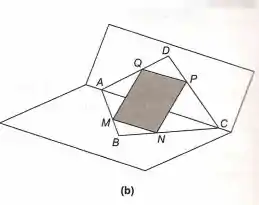
Antes de matarmos esse exercício, vamos relembrar o que ele nos pede:

Mostre que as quatro diagonais (as duas de ABCD e as duas de MNPQ) têm um ponto comum.

Beleza? Então, partiu!

Passo 2

Sabemos que

A M → = r M B →

Certo? Vamos abrir isso.

A M → = r M B → → M - A = r B - r M → M = r B + A r + 1

Seguindo o mesmo raciocínio

N = r B + C r + 1

P = r D + C r + 1

Q = r D + A r + 1

Dessa forma, podemos escrever

N M = C A r + 1   e   M Q = r B D r + 1 = N P

Portanto, ainda teremos M Q P N sendo um paralelogramo, certo?

As duas diagonais só podem se encontrar em um ponto no paralelogramo: o ponto médos dos lados opostos, vamos verificar então que ponto médio de M P é igual ao ponto médio de dois pontos opostos de A B C D , beleza?

M + P 2 = 1 2 r B + A r + 1 + r D + C r + 1 = r B + D + A + C 2 ( r + 1 )

Pronto, estamos quase acabando 😉.

Passo 3

Agora, vem o pulo do gato. Vamos usar o fato que em um paralelogramo A B C D , temos que D + C = A + B = 2 O , onde O é o ponto médio dos lados opostos, assim teremos que o ponto médio de M P , será:

r 2 O + 2 O 2 ( r + 1 ) = O 2 r + 1 2 ( r + 1 ) = O

Portanto, as diagonais do paralelogramo M Q P N se encontram no mesmo ponto que as diagonais de A B C D . Logo, as quatro diagonais tem o ponto O em comum.

FIM!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sendo a → = O A → e b → = O B → dois vetores não paralelos, escreva v → = O P → como combinação linear de a → e b → , sabendo que A P → = 2 3 A B →
A B C D é um quadrilátero, A D → = 3 v → ,B C → = 2 v → e A B → = w → . Que tipo de quadrilátero é A B C D ? Determine o lado C D → e as diagonais B D → e A C → em função de v → e w → .
Sejam vec u , vec v e vec w três vetores tais que vec u . vec v = vec v . vec w = vec u . vec w = 0 , |vec u| = sqrt(2) , |vec v| = 2 e |vec w| = 2 . Dados vec a = 2 vec u + vec v - vec w e vec b = ve
Determine as coordenadas da extremidade do segmento orientado que representa o vetor V = ( 3,0 , - 3 ) , sabendo-se que sua origem está no ponto P = 2,3 , - 5 .
Uma reta no plano tem equação y=2x+1. Determine um vetor paralelo a esta reta.