Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.2 - Ex. 16
Suponha que um vetor do plano aponte na direção que faz um ângulo de no sentido anti-horário a partir do eixo positivo e que um vetor daquele plano aponte na direção que faz um ângulo de no sentindo anti-horário a partir do eixo positivo. O que pode ser dito sobre o valor de ?
Passo 1
Vamos ilustrar o enunciado a fim de facilitar o entendimento:
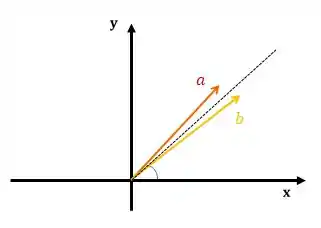
Como e são constituídos por entradas positivas (encontram-se no eixo e positivo), então podemos afirmar que .
Assim, como , o ângulo formado entre eles é agudo, o que é visível na imagem acima.
Resposta
Logo, podemos afirmar que o valor é maior do que zero.
Exercícios de Livros Relacionados
Encontre u → ⋅ v → , u → ⋅ u → e v → ⋅ v → . u → = 1 ,1 ,- 2 ,3 ,v → = ( - 1 ,0 ,5 ,1 ) u → = 2 ,- 1 ,1 ,0 , - 2 ,v → = ( 1 ,2 ,2 ,2 ,1 )
Sejam Σ 1 = ( O 1 ,e 1 → ,e 2 → ,e 3 → ) e Σ 2 = ( O 2 ,f 1 → ,f 2 → ,f 3 → ) sistemas de coordenadas tais que O 2 = 1 ,1 ,1 Σ 1 f 1 → = e 1 → + e 2 →f 2 → = e 2 →f 3 → = e 2 → + e 3 → Obtenha, em rel
Sejam Σ 1 = ( O 1 ,e 1 → ,e 2 → ,e 3 → ) e Σ 2 = ( O 2 ,f 1 → ,f 2 → ,f 3 → ) sistemas de coordenadas tais que O 2 = 1 ,0 ,0 Σ 1 f 1 → = e 1 →f 2 → = - e 3 →f 3 → = e 2 → Obtenha, em relação a Σ 2 ,a)
Em cada parte, encontre o vetor de coordenadas de w em relação à base S={ u 1 ,u 2 } .(a) u 1 = 1 ,- 1 ;u 2 =1 ,1 ,w = 1 ,0 .
Em cada parte, encontre o vetor de coordenadas de p em relação à base S={ p 1 ,p 2 ,p 3 } .(b) p =2 -x +x 2 ;p 1 =1 + x ,p 2 = 1 + x 2 ,p 3 =x + x 2