Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 9e
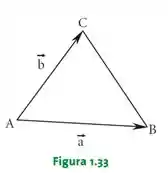
No triângulo ABC (Figura 1.33) seja e . Construir um representante de cada um dos vetores
e)
Passo 1
A gente vai começar separando esses vetores. O vetor é o próprio vetor da figura, já o vetor é a metade do vetor , com sentido oposto, graficamente fica assim:
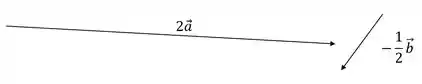
Passo 2
Agora é só somar os dois vetores
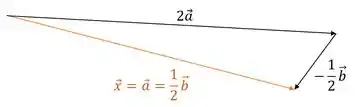
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
4.Prove que u → + z → = u → ⇒ z → = 0 → e que u → + z → = 0 →⇒z → = - u → . Essas propriedades asseguram a unicidade do elemento neutro e do elemento oposto.
8.a) Justifique a seguinte regra para determinar o vetor x → = u → + v → + w → , tornam-se representantes consecutivos, isto é, a origem de cada um coincidindo com a extremidade do anterior e “fecha-s
Considerando A , B , CeX como no exercício resolvido anterior, seja m a razão em queX divide ( A , B ) . Exprima C X → em função de C A → , C B → , m . Exprima p em função de m .
Sejam O A B C um tetraedro e X o ponto definido por B X → = m B C → . Exprima O X → e A X → em função de O A → , O B → ,O C →em .
Prove que o segmento que une os pontos médios das diagonais de um trapézio é paralelo às bases, e sua medida é a semidiferença das medidas das bases (figura 5-3 (b)).