Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 7

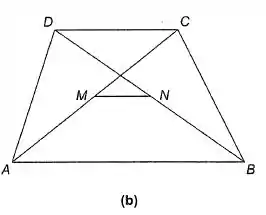
Prove que o segmento que une os pontos médios das diagonais de um trapézio é paralelo às bases, e sua medida é a semidiferença das medidas das bases (figura 5-3 (b)).

Passo 1

Bora lá! Usando as informações que foram dadas no enunciado, de cara já podemos notar que:

M N → = M D → +   D C → + C N → =   1 2 B D → +   D C → + 1 2 C A →

M N → = M B → +   B A → + A N → =   1 2 D B → +   B A → + 1 2 A C →

Passo 2

Agora, somando as duas equações, vamos ter:

2 M N → = 1 2 B D → + D C → + 1 2 C A → + 1 2 D B → + B A → + 1 2 A C →

Podemos reescrever a equação como,

2 M N → = 1 2 B D → + D C → + 1 2 C A → - 1 2 B D → + B A → - 1 2 A C →

Agora, dando aquela arrumada marota,

M N → = 1 2 D C → - 1 2 A B →

Colocando em evidência, temos

M N → = 1 2   D C → - A B →

Beleza?!

Se você reparar, A B → e D C → são paralelos. Portanto, o módulo da diferença é a diferença dos seus módulos, ou seja,

A B → - C D → =   A B → -   C D →

Então, o módulo de M N → é a semi-diferença das bases do trapézio, e como é escrito na forma

M N → = θ   D C → - A B →

Ele é paralelo a ambas as bases.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Decomponha W = - i → - 3 j → + 2 k → como a soma de dois vetores W 1 e W 2 , com W 1 paralelo ao vetor j → + 3 k → e W 2 ortogonal a este último.
Sejam V = i → + 2 j → - 3 k → e W = 2 i → + j → - 2 k → . Determine vetores unitários paralelos aos vetores (c) 2 V - 3 W
Demonstre que, se V e W são vetores quaisquer, então: (a): V . W = 1 4 ( V + W 2 - V - W 2 )
Demonstre que se V e W são vetores quaisquer, então: (c): V - W ≤ V - W ;
Demonstre que se V e W são vetores quaisquer, então: (a): V . W ≤ V W ;