Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 2.Exercício - Ex. 8
8.a) Justifique a seguinte regra para determinar o vetor , tornam-se representantes consecutivos, isto é, a origem de cada um coincidindo com a extremidade do anterior e “fecha-se o polígono”
b) Mostre que a regra do item a vale para quatro e cinco parcelas (é possível um número qualquer de parcelas usando o Princípio de indução finita)
c) Determine a soma dos vetores indicados em cada caso da figura 2-8.
Passo 1
Desenharemos os vetores consecutivos como a letra a), pede:
O vetor é igual a , vetor é igual a , vetor é igual a e vetor é igual a .
Agora vamos de até.
Vamos inicialmente de até , depois partimos para e finalmente de vamos para . Escrito vetorialmente é assim:
Substituindo:
Como imaginávamos!! Essa é a regra do polígono.
Passo 2
Agora vamos para a letra b).
Primeiro ele pede para fazermos com 4 vetores! Então, vamos lá:
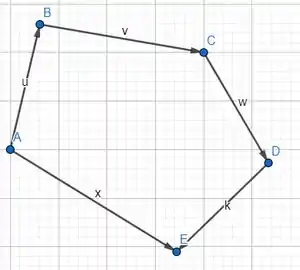
Temos que provar que
Da figura, temos:
Vamos de até !
Vamos de para , de para , de para , para .
Substituindo:
Agora para 5 vetores!
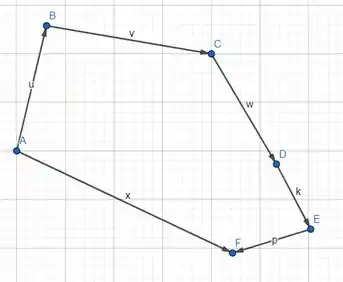
Temos que provar que
Da figura, temos:
Vamos de até!
Vamos de para , de para , de para , para e por fim de para .
Substituindo:
Pronto, demostramos para 4 vetores e para 5 vetores, essa regra serve para n vetores!!
Passo 3
Temos que “fechar polígonos” em todas as figuras
Vamos para a primeira.
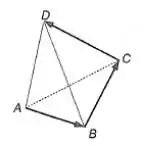
Para fechar o polígono com os vetores consecutivo, temos que desenhar o vetor. Então a soma desses vetores é.
Vamos para a segunda figura.
A soma que a gente quer é:
Só que e
Substituindo na expressão da soma, temos:
Então a soma dos vetores é igual a .
Vamos para a terceira figura:
A soma que a gente quer é:
Só que e . Substituindo tudo na expressão, temos:
Lembrando que :
Então, a soma dos vetores da figura é igual a
Agora vamos para a última:
Nessa figura, apenas precisamos completar o polígono, e para completar só falta a aresta .
Então a soma desses vetores da figura é igual a .
Resposta
c) Figura A:
Figura B:
Figura C:
Figura D: