Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.9 - Ex. 24
Use a Fórmula para encontrar a matriz canônica de uma rotação de radianos em torno do eixo determinado pelo vetor . [Observação: a Fórmula exige que o vetor que define o eixo de rotação tenha comprimento ].
Passo 1
Para começar temos que ter acesso a formula que é:
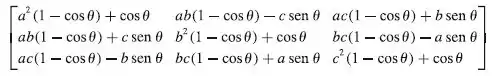
Sendo o ângulo de rotação do vetor:
Passo 2
Agora vamos lembrar que durante a os vetores usados na formula devem ser unitários então normatizando obtemos:
Como então:
Resposta
Exercícios de Livros Relacionados
Num dado dia, a qualidade do ar numa certa cidade é boa ou má. Os registros mostram que quando a qualidade do ar é boa num dado dia, então existe uma chance de 95% de que venha a ser boa no próximo di
Um rato num experimento de laboratório pode escolher um entre dois tipos de comida a cada dia: o tipo I ou tipo II. Os registros mostram que se o rato escolhe o tipo I num certo dia, então a chance de
Considere um processo de Markov com matriz de transiçãoO que representa a entrada 6 7 ?
Um rato num experimento de laboratório pode escolher um entre dois tipos de comida a cada dia: o tipo I ou tipo II. Os registros mostram que se o rato escolhe o tipo I num certo dia, então a chance de
Num certo instante de tempo inicial, havia 100.000 habitantes numa certa cidade e 25.00 habitantes nos arredores da cidade. A Comissão de Planejamento Regional detectou que, a cada ano, 5% da populaçã