Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.11 - Ex. 4
Use a matriz obtida para calcular . Confira suas respostas geometricamente esboçando os pontos .
Passo 1
O ponto preto é e o ponto rosa é os riscos azuis são pra indicar o plano .
Passo 2
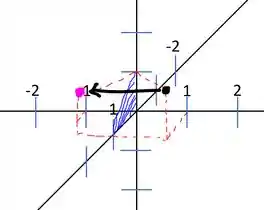
O ponto preto é e o ponto rosa é os riscos azuis são pra indicar o plano .
Passo 2
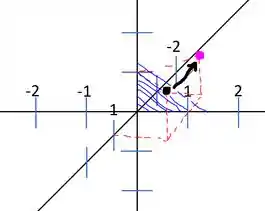
O ponto preto é e o ponto rosa é os riscos azuis são pra indicar o plano .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Identifique e esboce a cônica, conhecendo sua equação; 3 x 2 + 2 x y + 3 y 2 + 6 2 x + 2 2 y + 2 = 0 . x 2 + 4 y 2 + 3 3 x y - 1 = 0 . x 2 + 4 x y + 4 y 2 - 1 = 0 . 7 x 2 + 5 y 2 + 2 3 x y - 14 + 2 3
Em cada parte, encontre T ( x ) e expresse a resposta em forma matricial.
Num certo instante de tempo inicial, cada um de dois canais de televisão concorrentes, os canais 1 e 2, tem 50 % da audiência. A cada período de um ano, o canal 1 atrai 5 % da audiência do canal 2 e o
Prove que o produto de duas matrizes estocásticas é uma matriz estocástica. [Sugestão: escreva cada coluna do produto como uma combinação linear das colunas do primeiro fator.]
Se P for uma matriz estocástica regular com vetor de estado estacionário q , o que pode ser dito sobre a sequência de produtos P q ,P 2 q ,P 3 q , … ,P k q , … Quando k → ∞ ?