Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 23.Exercício - Ex. 4abcd

Identifique e esboce a cônica, conhecendo sua equação;

  1. 3 x 2 + 2 x y + 3 y 2 + 6 2 x + 2 2 y + 2 = 0 .
  2. x 2 + 4 y 2 + 3 3 x y - 1 = 0 .
  3. x 2 + 4 x y + 4 y 2 - 1 = 0 .
  4. 7 x 2 + 5 y 2 + 2 3 x y - 14 + 2 3 x - 10 + 2 3 y + 8 + 2 3 = 0 .
  5. 7 x 2 + 6 x y - y 2 + 28 x + 12 y + 28 = 0 .
  6. 16 x 2 - 108 x y - 29 y 2 + 260 = 0 .
  7. 5 x 2 + 2 y 2 + 2 x y + 2 = 0 .

Passo 1

  1. Vamos começar pela translação dos eixos para eliminar os termos lineares.

    2. Para a cônica em questão, a = 3 ,   b = 2 ,   , c = 3 ,   d = 6 2 ,   e = 2 2 e f = 2 .

    Vamos escrever a matriz dos coeficientes:

    M 3 = a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f = 3 1 3 2 1 3 2 3 2 2 2

    As duas primeiras linhas nos permitem escrever

    3 h + k + 3 2 = 0 h + 3 k + 2 = 0 ⟹ h = - 2   e   k = 0

    A última linha nos permite calcular o novo termo independente:

    f ' = 3 2 ⋅ h + 2 ⋅ k + 2 = 3 2 - 2 + 2 = - 4

    ∴ f ' = - 4

    Assim, a equação da cônica após a translação fica

    g x , y = 3 x 2 + 2 x y + 3 y 2 - 4

    Passo 2

    Agora, devemos fazer a rotação de um ângulo θ . Sabemos que

    cot ⁡ 2 θ = c - a b = 3 - 3 2 = 0 ⟹ 2 θ = 90 ° ∴ θ = 45 °

    Assim,

    a ' + c ' = a + c a ' - c ' = b sin ⁡ 2 θ ⟹ a ' + c ' = 3 + 3 a ' - c ' = 2 sin ⁡ 2 × 45 ° ⟹ a ' + c ' = 6 a ' - c ' = 2 ∴ a ' = 4   e   c ' = 2

    A nova equação fica:

    4 x 2 + 2 y 2 - 4 = 0 ∴ x 2 + y 2 2 = 1

    Agora, conseguimos enxergar que a equação representa uma elipse.

    Passo 3

    Esboço da curva

    Passo 4

  2. Não precisamos fazer a translação de eixos nesse caso, pois não há termos lineares.

    3. Nos resta fazer a rotação de eixos. Temos que

    cot ⁡ 2 θ = c - a b = 4 - 1 3 3 = 1 3 ⟹ 2 θ = 60 ° ∴ θ = 30 °

    Assim,

    a ' + c ' = a + c a ' - c ' = b sin ⁡ 2 θ ⟹ a ' + c ' = 5 a ' - c ' = 3 3 sin ⁡ 60 ° ⟹ a ' + c ' = 5 a ' - c ' = 6 ∴ a ' = 11 2   e   c ' = - 1 2

    Portanto, temos a nova equação:

    11 2 x 2 - 1 2 y 2 - 1 = 0 ⟹ 1 2 y 2 - 11 2 x 2 = 1

    que representa uma hipérbole.

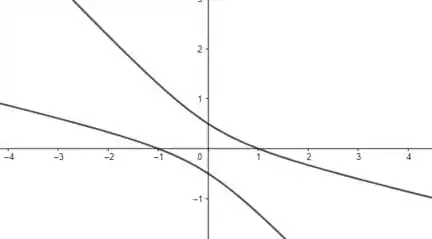
    Passo 5

  3. Note que podemos fatorar a expressão

    4. 4 y 2 + 4 x y + x 2 - 1 = 0 ⟹ x + 2 y 2 - 1 = 0 ⟹

    x + 2 y - 1 x + 2 y + 1 = 0

    Assim, temos a reunião de duas retas paralelas: x + 2 y - 1 = 0 e x + 2 y + 1 = 0 .

    Passo 6

  4. Aqui, vamos precisar eliminar os termos lineares.

Para a cônica em questão, a = 7 ,   b = 2 3 ,   c = 5 ,   d = - 14 + 2 3 ,   e = - 10 + 2 3 , e f = 8 + 2 3 . Podemos montar a matriz

M 3 = a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f = 7 3 - 7 - 3 3 5 - 5 - 3 - 7 - 3 - 5 - 3 8 + 2 3

Assim, temos o sistema

7 h + 3 k - 7 - 3 = 0 3 h + 5 k - 5 - 3 = 0 ⟹ h = 1   e   k = 1

Portanto,

f ' = - 7 - 3 h + - 5 - 3 k + 8 + 2 3 = - 4

A nova equação da cônica será:

g x , y = 7 x 2 + 2 3 x y + 5 y 2 - 4

Passo 2

Agora, devemos eliminar o termo misto. Segue:

cot ⁡ 2 θ = a - c b = 7 - 5 2 3 = 1 3 ⟹ 2 θ = 60 °

Assim,

a ' + c ' = a + c a ' - c ' = b sin ⁡ 2 θ ⟹ a ' + c ' = 12 a ' - c ' = 4 ⟹ a ' = 8   e   c ' = 4

Portanto, temos

8 x 2 + 4 y 2 - 4 = 0 ⟹ 2 x 2 + y 2 = 1

Que representa uma elipse!

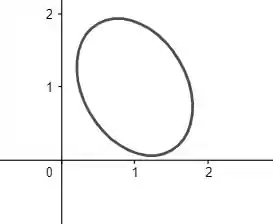
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, encontre a matriz canônica do operador T:R 3→R 3 que transforma cada ponto ( x ,y , z ) reflexão no plano x z .
Em cada parte, encontre a matriz canônica do operador T:R 3→R 3 que efetue a rotação de cada vetor por 90 ° no sentido anti-horário em torno do eixo z (olhando ao longo do eixo z positivo para a orige
Em cada parte, encontre a matriz 2 x 2 que efetua umcisalhamento(a) de fator k=4 na direção y .(b) de fator k= - 2 na direção x .
Em cada parte, encontre a matriz canônica do operador T:R 3→R 3 que transforma cada ponto ( x ,y , z ) reflexão no plano x y .
Em cada parte, encontre a matriz canônica do operador T:R 2→R 2 que transforma cada ponto ( x ,y ) na projeção ortogonal sobre o eixo y .