Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.Exercícios Suplementares - Ex. 10
Para uso neste exercício, definimos uma “matriz ” como sendo uma matriz quadrada com um número ímpar de linhas e colunas que tem 0 em cada entrada, exceto nas diagonais principal e secundária, onde tem todas entradas iguais a 1. Encontre o posto e a nulidade das matrizes a seguir
a)
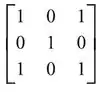
b)
c) A matriz de tamanho
Passo 1
(a)
Vamos lá! temos de entender que essa matriz se trata de um tipo especial de matriz simétrica, que tem uma linha central que funciona como espelho e a partir dela a matriz se torna uma reflexão da primeira metade, como no exemplo a seguir:
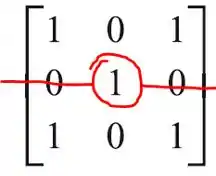
Nossa linha de reflexão.
Assim temos que a segunda metade da matriz simplificada vai ser totalmente nula.
Sabendo que o posto é a quantidade de linhas não nulas e a nulidade é a quantidade de linhas nulas.
Assim temos:
Passo 2
(b)
Seguindo a mesma lógica do item anterior temos:
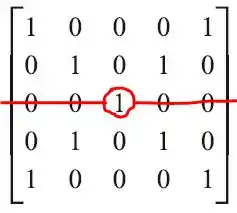
Sendo o posto é a quantidade de linhas não nulas e a nulidade é a quantidade de linhas nulas.
Assim temos:
Passo 3
(c)
Vamos lá! Seguindo a lógica do item (a) temos:
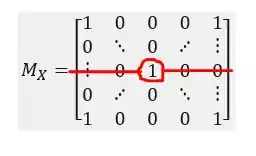
Sendo o posto é a quantidade de linhas não nulas e a nulidade é a quantidade de linhas nulas sendo o número de linhas e colunas .
Assim temos:
Resposta
(a)
(b)
(c)