Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.3 - Ex. 11
Nos exercícios 9-12 encontre uma forma ponto-normal da equação do plano que passa por P e nem como normal
Passo 1
Vamos fazer um desenho esquemático do problema:
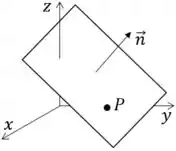
Para determinar a equação do plano utilizamos o Equação (2) da Seção 3.3, que diz que para um ponto e um vetor o plano normal a ele é:
Passo 2
A questão nos dá os seguintes ponto e vetor:
Então vamos aplicar os valores do vetor e do ponto na equação:
Chegamos na equação do plano:
Resposta
Exercícios de Livros Relacionados
Seja V o conjunto dos pares ordenados de números reais. Definamos: x 1 , y 1 + x 2 , y 2 =2 x 1 - 2 y 1 , - x 1 + y 1 a x , y = ( 3 a y , - a x ) Com essas operações definidas sobre V , perguntamos se
Seja V o conjunto dos pares ordenados de números reais. V não é um espaço vetorial em relação a nenhum dos dois seguintes pares de operações sobre V :a) x 1 , y 1 + x 2 , y 2 =x 1 + x 2 , y 1 + y 2 e
Sabendo que V = x , y x , y∈ R } anterior definamos a adição como o fazemos habitualmente no R 2 e a multiplicação por escalares assim: a x , y = a x ,0 . É então V um espaço vetorial sobre R ? Por qu
Seja V = x , y x , y ∈ C . Mostrar que V é um espaço vetorial sobre R com a adição e a multiplicação por escalares definidas assim x 1 , y 1 + x 2 , y 2 =x 1 + x 2 , y 1 + y 2 , ∀ x 1 , y 1ex 2 , y 2∈
No espaço vetorial P 3 R sejam dados os vetores f t = t 3 - 1 , g t = t 2 + t - 1eh t = t + 2 .a) Calcular 2 f t + 3 g t - 4 h ( t ) b) Existe k ∈ R de maneira que f t + k g t = h ( t ) ?c) Existem k