Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 47a

Prove que são verdadeiras as afirmações seguintes.

(a) , quaisquer que sejam os pontos A, B, C e D (Relação de Euler).

Passo 1

Bora lá!

Para começarmos a nossa resolução, vamos considerar os pontos A, B, C e D, e seus respectivos vetores, os quais, para facilitar o entendimento da questão, serão dispostos segundo a figura abaixo:

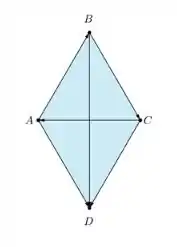
Passo 2

Primeiramente, ao analisarmos a nossa figura, podemos notar que cada um dos vetores pode ser escrito pela soma ou subtração de outros dois. Ou seja, tomando como exemplo o vetor , temos:

Beleza?

Dessa forma, partiremos da igualdade do enunciando e substituiremos os termos por outros equivalentes, através do método descrito acima. Assim, temos:

Passo 3

Agora, vamos aplicar a nossa já conhecida propriedade distributiva e, especificamente no último termo, trocaremos por , obtendo:

Resposta

Portanto, de fato,

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostrar que, se u → é ortogonal a v → e w → , u → também é ortogonal a v → + w → .

Determinar u → . v → + u → . w → + v → . w → , sabendo que u → + v → + w → = 0 , u → = 2 ,v → = 3 e w → = 5 .

Sabendo que u → = 2 ,v → = 3 e que u → e v → formam um ângulo de 3 π 4r a d , determinar 2 u → - v → . u → - 2 v → .

Calcular o módulo dos vetores u → + v → e u → - v → , sabendo que u → = 4 , v → = 3 e o ângulo entre u → e v → é de 60 ° .

Se o vetor A B → tem co-senos diretores p ,q e r e ângulos diretores α ,β e γ , quais são os co-senos e os ângulos diretores de B A → ?