Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Mínimos Quadrados e Projeções

Ver Todos os Exercícios

Teoria

Lembra que quando aprendemos o método de Mínimos Quadrados o que estávamos achando era de fato a melhor aproximação possível? Ou, em outras palavras, o vetor mais próximo do nosso b que satisfazia a equação.

E, como também discutimos lá, o menor caminho que liga dois vetores é sempre uma reta, dessa forma, a ideia dos Mínimos Quadrados está intimamente conectada à ideia de projeção!!

Já vimos como encontrar a projeção de um vetor por meio de sua T L . Agora, vamos ver como fazer isso por meio de mínimos quadrados (fica MUITO mais rápido haha).

Ou seja, resolvemos o sistema A T A z = A T b . Aquele que vimos em mínimos quadrados, só troquei o x pelo z aqui ;).

Depois, multiplicamos o vetor z obtido da solução do sistema pela matriz A , e temos a sua projeção!

Vamos ver um exemplo:

Considere H = s p a n 1 2 3 , 4 1 - 2 e b = 2 0 0 . Calcule P H b .

Definindo A = 1 4 2 1 3 - 2 , basta resolver:

A T A z = 1 2 3 4 1 - 2 1 4 2 1 3 - 2 z = 1 2 3 4 1 - 2 2 0 0 = A T b

14 0 0 21 z = 2 8

z = 1 7 8 21

Sendo assim,

P H b = A z = 1 4 2 1 3 - 2 1 7 8 21 = 5 3 2 3 - 1 3

Obs1: Se a base H é ortogonal, o produto A T A será uma matriz diagonal e o sistema será resolvido facilmente. Foi o que aconteceu nesse exemplo.

Obs2: Se a base H é ortonormal, temos que P H = A A T . A projeção de b sobre H é então dada por P H b = A A T b

Obtendo a matriz Projeção

Apesar desse método ser mais voltado para obter diretamente a projeção de um vetor determinado, podemos obter a matriz projeção em uma direção v pela fórmula:

P v = v v T v T v

Essa fórmula é uma consequência direta da de mínimos quadrados. É importante frisar que essa fórmula só funciona para projeções sobre uma reta, que é gerada por um único vetor.

Tá meio esquisito isso de v e v T né? Vamos fazer um exemplo pra deixar mais claro então:

Determine a matriz da projeção sobre a reta x + 3 y = 0 no R 2 :

Vamos achar o vetor gerador dessa reta, para aplicar na fórmula acima:

x + 3 y = 0 ⟹ x = - 3 y

x , y = - 3 y , y = y ( - 3,1 )

P v = v v T v T v = - 3 1 - 3 1 - 3 1 - 3 1 = 9 - 3 - 3 1 10 = 9 10 - 3 10 - 3 10 1 10

Facilitou bastante nossa vida não é mesmo? Mas não é só isso, tenho mais um macete matador pra você!

Acabamos de aprender como obter a matriz projeção em um subespaço de dimensão 1 . Mas também podemos fazer uma pequena adaptação nela pra obtermos a matriz que projeta um vetor sobre o complemento ortogonal de uma reta!

Ficou confuso? Calma que vou explicar! Imagine que você quer projetar sobre um plano no R 3 . Basta você encontrar o complemento ortogonal desse plano (que será uma reta), aplicar aquela fórmula pra achar a matriz que projeta nessa reta. Por fim, você a subtrai da matriz identidade!

P H ⊥ = I - P H

Dá uma olhada nesse desenho pra ver se ajuda ;)

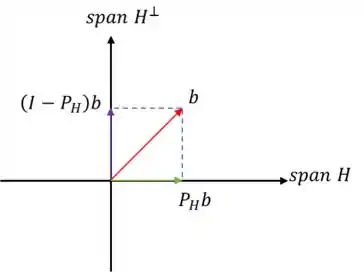
Obs.: Outra coisa muito interessante que esse desenho nos diz é que a soma vetorial de P H b com P H ⊥ b vale o próprio b !!

Então se eu quiser saber a matriz projeção no complemento ortogonal da reta x + 3 y = 0 do último exemplo, é só fazer a seguinte operação de matrizes:

P H ⊥ = I - P H

P H ⊥ = 1 0 0 1 - 9 10 - 3 10 - 3 10 1 10 = 1 10 3 10 3 10 9 10

Nos exercícios vão ter alguns exemplos pra você praticar isso. Vai ver que é bem mais rápido que por T L . A principal diferença entre os métodos é que por matrizes você encontra diretamente o vetor projetado, e ele é normalmente mais rápido. Por outro lado, usando a T L você encontra uma fórmula que pode ser usada com qualquer vetor, apesar de perder mais tempo.

Você pode usar o que se sentir mais confortável usando, mas fique atento, pois em alguns casos pode ser muito mais favorável ir por um dos métodos.

Obtendo a matriz Projeção

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 162 – Prob 5.5 Adaptado

Determine as matrizes das T L s T : R n → R n :

a   n = 2 , projeção ortogonal na reta 2 t , - t ∈ R 2 ; p a r a   t ∈ R

b   n = 3 , projeção ortogonal sobre o plano x = z

c   n = 2 , projeção ortogonal na reta 2 x - 4 y = 0

d   n = 3 , projeção ortogonal no plano x + y - z = 0

Passo 1

a É pedida a matriz que representa a projeção sobre a reta gerada pelo vetor 2 , - 1 .

A fórmula da matriz projeção sobre a direção de um vetor v é dada por:

P v = v v T v T v = 2 - 1 2 - 1 2 - 1 2 - 1 = 4 - 2 - 2 1 5 = 4 5 - 2 5 - 2 5 1 5

Passo 2

b   Queremos achar um a projeção sobre um plano no R 3 . Repare que o complemento ortogonal do plano será uma reta. Logo, podemos usar nossa fórmuleta!

Da equação do plano, podemos encontrar o vetor gerador da reta ortogonal à ele:

x - z = 0

1,0 , - 1

Vamos achar a matriz que representa a projeção sobre essa reta:

P v = v v T v T v = 1 0 - 1 [ 1 0 - 1 ] [ 1 0 - 1 ] 1 0 - 1 = 1 0 - 1 0 0 0 - 1 0 1 2 = 1 2 0 - 1 2 0 0 0 - 1 2 0 1 2

Para encontrarmos a matriz que projeta sobre o plano basta fazermos:

P H = I - P v

P H = 1 0 0 0 1 0 0 0 1 - 1 2 0 - 1 2 0 0 0 - 1 2 0 1 2 = 1 2 0 1 2 0 1 0 1 2 0 1 2

Passo 3

c Primeiro passo é achar o vetor que gera essa reta. Temos pela equação da mesma que:

2 x = 4 y ⇒ x = 2 y

Logo, o vetor genérico é da forma 2 y , y = y 2,1 . Ou seja, é uma projeção na direção do vetor 2,1 . E temos uma fórmula pra isso ;)

P v = v v T v T v = 2 1 2 1 2 1 2 1 = 4 2 2 1 5 = 4 5 2 5 2 5 1 5

Passo 4

d Queremos achar um a projeção sobre um plano no R 3 . Repare que o complemento ortogonal do plano será uma reta. Logo, podemos usar nossa fórmuleta!

Da equação do plano, podemos encontrar o vetor gerador da reta ortogonal à ele:

x + y - z = 0

1,1 , - 1

Vamos achar a matriz que representa a projeção sobre essa reta:

P v = v v T v T v = 1 1 - 1 [ 1 1 - 1 ] [ 1 1 - 1 ] 1 1 - 1 = 1 1 - 1 1 1 - 1 - 1 - 1 1 3 = 1 3 1 3 - 1 3 1 3 1 3 - 1 3 - 1 3 - 1 3 1 3

Para encontrarmos a matriz que projeta sobre o plano basta fazermos:

P H = I - P v

P H = 1 0 0 0 1 0 0 0 1 - 1 3 1 3 - 1 3 1 3 1 3 - 1 3 - 1 3 - 1 3 1 3 = 2 3 - 1 3 1 3 - 1 3 2 3 1 3 1 3 1 3 2 3

Resposta

a   4 5 - 2 5 - 2 5 1 5

b   1 2 0 1 2 0 1 0 1 2 0 1 2

c   4 5 2 5 2 5 1 5

d 2 3 - 1 3 1 3 - 1 3 2 3 1 3 1 3 1 3 2 3

Exercício Resolvido #2

Lista 5 de monitoria para a p2, Álgebra Linear I, 2015.1, exercício 1-b), PUC-rio.

Sejam u = 1,2 , 2 ,   v = 1,1 , 0 e   w = ( 1,0 , 1 ) vetores do R 3 . Calcule a projeção ortogonal de u em H = s p a n { v , w } , utilizando o método dos mínimos quadrados, sabendo que u ∉ s p a n { v , w } .

Passo 1

Bom, como queremos saber a projeção do vetor b = 1,2 , 2 sobre H , podemos usar nossa fórmula. Como H = 1,1 , 0 , 1,0 , 1 , definimos A = 1 1 1 0 0 1 , e resolvemos:

A T A z = 1 1 0 1 0 1 1 1 1 0 0 1 z = 1 1 0 1 0 1 1 2 2 = A T b

2 1 1 2 z = 3 3

2 1 1 2 3 3 → L 2 ← 2 L 2 - L 1 2 1 0 3 3 3 ⇒ 2 x = 3 - y = 2 ⇒ x = 1 ⇒ y = 1

z = 1 1

Por fim, temos que:

P H b = A z = 1 1 1 0 0 1 1 1 = 2 1 1

Resposta

P H 1,2 , 2 = ( 2,1 , 1 )

Exercício Resolvido #3

PUCRIO-P2-2015.1-2c

Sejam H = s p a n 1 , 1,0 , 0,1 , 1 e P H : R 3 ⟶ R 3 a projeção ortogonal sobre H . Use o método dos mínimos quadrados para calcular P H ( 1,1 , 1 ) .

Passo 1

Definimos a matriz A e o vetor b como:

A = 1 0 1 1 0 1 ; b = 1 1 1

Sendo assim,

A T = 1 1 0 0 1 1

Agora basta aplicarmos mínimos quadrados:

A T A z = 1 1 0 0 1 1 1 0 1 1 0 1 z = 1 1 0 0 1 1 1 1 1 = A T b

2 1 1 2 z = 2 2

Montando o sistema:

2 x 1 + x 2 = 2 x 1 + 2 x 2 = 2       I I I

Fazendo - 2 I + ( I I ) :

- 3 x 1 = - 2 ⇒ x 1 = 2 3

E substituindo em ( I I ) :

2 3 + 2 x 2 = 2 ⇒ 2 x 2 = 4 3 ⇒ x 2 = 2 3  

Passo 2

Ainda não acabou! Falta calcular a projeção! Para isso, basta fazer:

P H b = A z = 1 0 1 1 0 1 2 3 2 3 = 2 3 4 3 2 3

E assim, P H 1 , 1,1 = 2 3 , 4 3 , 2 3

Resposta

P H 1,1 , 1 = 2 3 , 4 3 , 2 3

Exercício Resolvido #4

UFRJ-P4-2015.2.1

Seja { a 1 → , a 2 → , … , a n → } uma base do subespaço H ⊂ R m e defina a matriz A m × n cuja j-ésima coluna é a j → . A projeção ortogonal de um vetor b → sobre um subespaço H ,   P H ( b → ) , é dada por:

a   A T A - 1 A T b →

b   I - A A T A - 1 A T b →

c   I - A T A - 1 A T b →

d   A A T A - 1 A T b →

Passo 1

Bom, pelas respostas sabemos que o enunciado está utilizando mínimos quadrados para projetar o vetor. Vamos dar uma relembrada rapidinho no método:

A T A z → = A T b →

Isso é penas o método dos mínimos quadrados. Sabemos que a projeção é somente:

P H b → = A z →

Mas repare que se você isolar o z nos mínimos quadrados, teremos:

z → = A T A - 1 A T b →

Passo 2

Se você perceber, temos esse termo A T A - 1 A T b → escrito em todas as letras, agora basta irmos substituindo e vermos o termo que vai dar A z → , afinal P H b → = A z → .

Se fizermos isso na letra ( a ) teremos apenas z → , que não é a projeção de b → .

Se fizermos isso na letra ( b ) , vamos ter I - A z → que também não é a projeção de b → .

Na letra ( c ) também vamos ter apenas I - z →

Entretanto na letra ( d ) , teremos A z → que é exatamente a projeção de b → !

Resposta

Letra ( d )

Exercícios de Livros Relacionados

1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1
3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.
4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?
2. Seja u o centróide dos vetores u 1 , u 2 , … , u p do R n . Calcular nos exemplos do exercício 1 a soma u - u 1 2 + … + u - u p 2 .
Qual é a série de Fourier de s e n (3 x) ?