Exercícios de Mínimos Quadrados e Projeções - Lista de Exercícios Resolvida

Seja uma base do subespaço e defina a matriz cuja j-ésima coluna é . A projeção ortogonal de um vetor sobre um subespaço , é dada por:

Determine as matrizes das

, projeção ortogonal na reta

, projeção ortogonal sobre o plano

, projeção ortogonal na reta

, projeção ortogonal no plano

Sejam vetores do . Calcule a projeção ortogonal de em , utilizando o método dos mínimos quadrados, sabendo que .

Sejam e a projeção ortogonal sobre . Use o método dos mínimos quadrados para calcular .

Ajustando-se uma reta aos dados abaixo:

Obtêm-se os coeficientes e . Use esta informação para calcular , a projeção ortogonal de sobre o complemento ortogonal de , onde

À questão “Em , determine a projeção ortogonal de sobre o plano gerado pelos vetores e ”, Andrezinho respondeu da seguinte maneira:

Defina o que é a projeção ortogonal sobre um subespaço .

Determine a projeção ortogonal de sobre o plano .

Andrezinho respondeu que a projeção ortogonal de é um vetor de ! Explique o erro de Andrezinho e a que vetor corresponde.

Calcule a distância de à sua projeção sobre o plano .

A projeção ortogonal do vetor sobre o plano é o vetor:

Seja uma base do subespaço e defina a matriz cuja j-ésima coluna é . A projeção ortogonal de um vetor sobre um subespaço , é dada por:

Seja o vetor do plano que é o mais próximo do vetor . Então a soma de suas entradas , vale:

Considere as seguintes afirmações:

1. Se é um conjunto ortonormal que gera o subespaço , então é uma base ortogonal de .
2. O sistema linear sempre tem solução mesmo quando

Qual das opções abaixo é CORRETA?

A afirmativa é verdadeira e é verdadeira

A afirmativa é verdadeira e é falsa

A afirmativa é falsa e é verdadeira

A afirmativa é falsa e é falsa

Sejam e . Use o fato de que é uma solução no sentido dos mínimos quadrados de para calcular , a projeção ortogonal de sobre o espaço-coluna de .

Calcule a projeção ortogonal do vetor sobre o espaço gerado por e

(a)

(b)

(c)

(d)

Seja e . A soma das coordenadas do vetor de mais próximo de é:

Seja um subespaço de e . Sejam e as projeções de em e , respectivamente:

é verdadeira, mas é falsa

e são verdadeiras

e são falsas

é falsa, mas é verdadeira

Seja o ponto do plano mais próximo de . A distância de a é:

Sejam um espaço vetorial com produto interno e o conjunto linearmente independente e seja a projeção de em . Então:

é ortogonal a

é ortogonal a

Sejam uma matriz quadrada e a imagem de . É dado que a solução geral do sistema é , com . É correto afirmar que , a projeção ortogonal de sobre é sempre igual a:

Calcule a projeção ortogonal do vetor no plano gerado pelos vetores e :

Sejam e a projeção ortogonal sobre . Use o método dos mínimos quadrados para calcular .

Considere o produto interno usual do . Calcule a projeção ortogonal do vetor à reta na direção do vetor :

Sejam e vetores do e o ângulo entre eles:

1. Se , então é ortogonal ao vetor
2. Se os componentes de são todos menores que , em módulo, então

Ambas são verdadeiras.

Ambas são falsas.

é verdadeira e é falsa.

é falsa e é verdadeira.

Seja e e

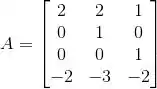
tal que . Então a projeção ortogonal de sobre a imagem de é:

(a)

(b)

(c)

(d)

Seja o conjunto solução do sistema

Compute a projeção ortogonal de sobre .

Considere o produto interno usual de . Calcule a projeção ortogonal do vetor no plano