Calcule as reações nos apoios e da viga abaixo sabendo que a viga está apoiada por duas molas lineares horizontais e duas verticais. Dado:;
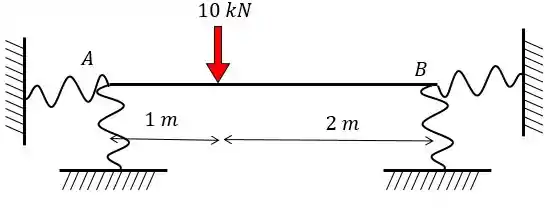
Passo 1
Pessoal, vamos resolver essa questãozinha que tem uma viga em condição hiperestática e possui duas molas, como dito no enunciado. Uhullll
A primeira coisa que a gente tem que lembrar é que vamos retirar as molas e substituir por apoios fixos. Dessa forma a nossa resolução fica mais fácil pois resolvermos um problema hiperestático normal. Depois, lá no final do problema a gente calcula a parcela relativa aos apoios elásticos e soma tudo.
Vamos ver com calma tudo isso, partiu!
Passo 2
Vamos retirar as molas e substituí-las por outros tipos de apoio. Como os apoios estão restritos tanto no eixo vertical quanto no eixo horizontal pelos elásticos então vamos substituir por apoios de segundo gênero. Dessa forma a gente vai ter o seguinte:
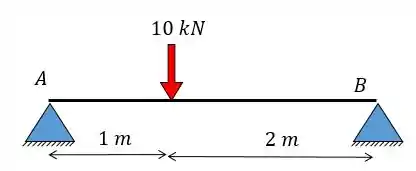
Pronto! Chegamos no nosso problema hiperestático convencional. Agora vamos resolvê-lo normalmente.
Passo 3
Este problema hiperestático possui um grau de hiperestaticidade, então vamos quebrar um vínculo (pode ser qualquer um, eu vou quebrar o apoio ) a gente só precisa lembrar que temos de colocar uma força equivalente. Dessa forma vamos obter:
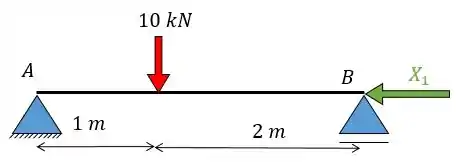
Eis que temos o nosso hiperestático e agora o que temos que fazer é achar o valor desse “indivíduo” escrutável... Para isso vamos dividir o problema em dois sistemas e fazer os seus respectivos diagramas de momento fletor.
Ps: Como, ao dividirmos o problema em dois sistemas, a gente obtém sistemas isostáticos, não vou perder muito tempo fazendo as contas não ok? Só vou mostrar como que fica o resultado para vocês =D
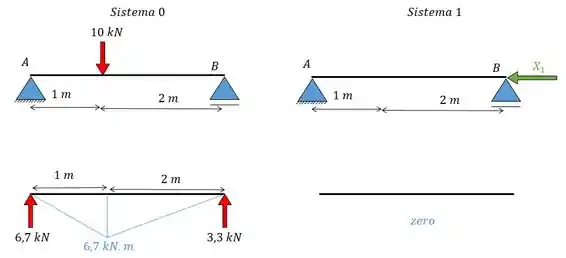
Viram como eu sou bonzinho e além de colocar o diagrama do momento fletor (em azul) ainda coloquei as forças resultantes (em vermelho). Owwnnnnn, que fofis....
Passo 4
Agora a gente tem que lembrar de como calcular o nosso hiperestático . A gente faz isso através da equação do deslocamento que tem a seguinte forma:
Então a gente vai precisar achar a deformação do sistema 0 em relação ao sistema 1 () e do sistema 1 em relação a ele mesmo (). Lembrando que vamos fazer isso com ajuda daquela nossa tabelinha marota. Mas reparem numa coisa, o momento para o caso do sistema 1 é nulo então vamos ter:
Pessoal, achamos os valores de e já podemos substituir na expressão abaixo?
A resposta é não =(
Por que a resposta é não? Porque se fizéssemos isso então a gente não estaria considerando a parte dos apoios elásticos, que até agora ainda não apareceram...
Essa é a diferença dos exercícios com molas. Quando não tem mola, os temos EJCδ são iguais a combinação dos diagramas. Quando tem mola, esses termos são compostos pela combinação dos diagramas + as parcelas referentes às molas. Vamos ver como fica isso.
Passo 5
Para considerarmos a parte relativa aos apoios elásticos nós vamos calcular um novo e um novo , vamos chamá-los de e . Esses novos termos são as deformações de cada apoio elástico e são dados por aquelas equações que vimos na teoria:
Mas nesse caso, não temos molas rotacionais, só molas lineares. Então fica assim:
Ou seja, com as reações de apoio NOS PONTOS ONDE FICAM AS MOLAS, nós vamos poder calcular os valores e . Vamos olhar novamente as reações da nossa viga:
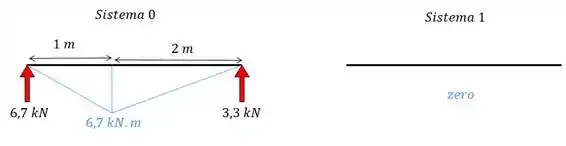
Mas como no sistema 1, as reações de apoio são nulas nos 2 pontos onde temos molas (A e B), então vamos ter:
No caso da combinação , que só usamos o sistema 1, também vai ficar tudo nulo:
Passo 6
Então o que podemos assumir deste exercício?
Como todos os deslocamentos são nulos então de fato o nosso hiperestático é nulo:
Sendo assim, basta substituir na nossa viga e achar as reações normalmente. Lembrando que o nosso hiperestático representa o valor de :
Passo 7
Dessa forma vamos ter:
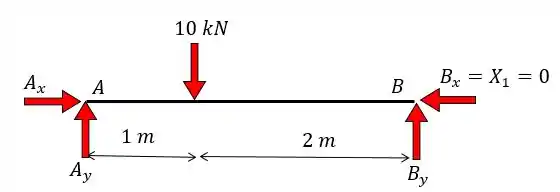
Pelas equações da estáticas vamos achar: