Determine a rotação do ponto A e o deslocamento vertical do ponto B da estrutura dada abaixo.
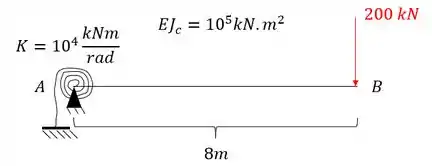
Passo 1
Nós não sabemos trabalhar bem com molas, mas sabemos trabalhar muito bem com apoios, por isso vale lembrar sempre a seguinte regrinha.
- Molas verticais e horizontais sempre irão virar apoios do primeiro gênero
- Molas do tipo engaste elástico sempre irão virar apoios com momentos fletores, podendo ser carrinhos ou engastes dependendo da situação.
No nosso exemplo, podemos ver que temos uma mola do tipo engaste elástico do lado esquerdo, que junto com o apoio do segundo gênero irá equivaler a um engaste.
Sendo assim a nossa estrutura equivalente será:
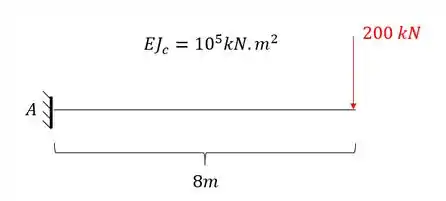
Passo 2
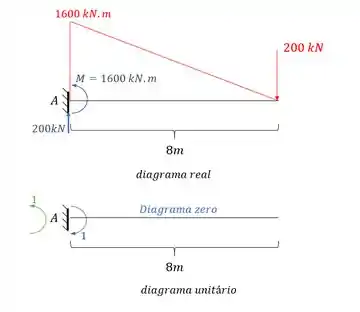
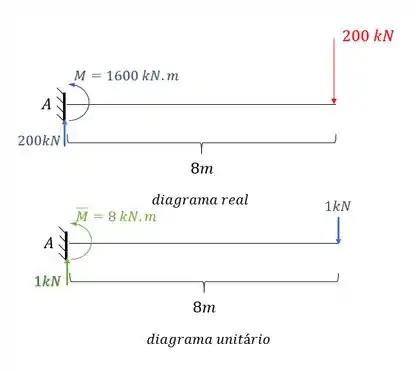
Perceba que nesse nosso primeiro exemplo a estrutura de fato é isostática. E agora basta fazermos o que já sabemos para determinar a deformação normal dessa estrutura, sabemos que o primeiro diagrama a ser determinado é o de momentos fletores devido a carga real na nossa estrutura, que será dada por:
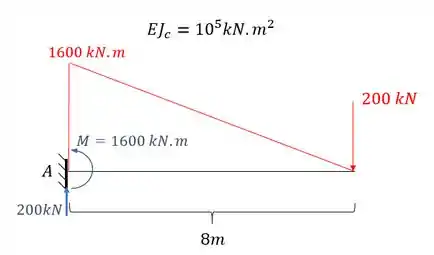
Perceba que também colocamos as reações de apoio que vão ser bem importantes pra gente.
A partir desse gráfico, podemos analisar cada item do enunciado separadamente.
Passo 3
O primeiro objetivo é determinar a rotação do ponto A.
- Rotação no ponto A
- Deformação relacionada a mola em A
- Deformação total será a soma de todas as parcelas contribuintes da deformação.
- Deslocamento vertical no ponto B
- Deformação da mola em A devido uma carga em B
- Deformação total será a soma de todas as parcelas contribuintes da deformação.
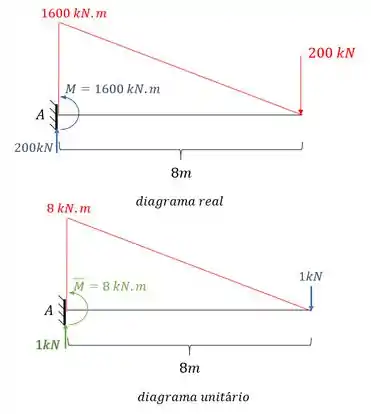
Como já temos o diagrama com carregamento real, precisamos do diagrama colocando no ponto A um momento que represente a rotação no ponto A:
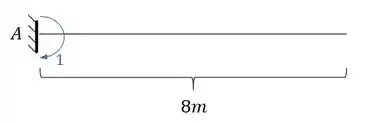
E o diagrama será dado por:
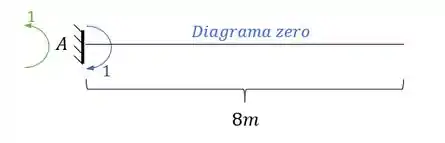
E perceba que o diagrama nesse caso será zero. Mas as reações de apoio para nós serão importantes.
Passo 4
Perceba que se combinarmos os diagramas teremos que:
Mas perceba que isso são as deformações apenas relativas ao diagrama de momentos, vamos agora contabilizar o que se refere as molas, ou seja, em um primeiro momento isso pode parecer que a rotação será zero. Mas precisamos tomar cuidado, porque temos a mola, sendo assim teremos que.
Como se trata de uma mola do tipo engaste elástico, sabemos que a sua fórmula é dada por.
Sabemos que:
Substituindo teremos que:
Passo 5
O segundo objetivo é determinar o deslocamento vertical em B.
Como já temos o diagrama com carregamento real, precisamos do diagrama colocando no ponto B uma carga vertical que represente o deslocamento no ponto B:
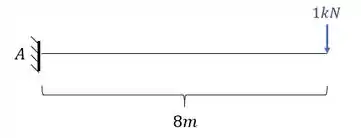
E o diagrama será dado por:
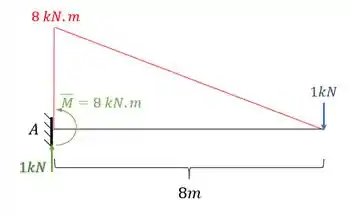
Passo 6
Perceba que se combinarmos os diagramas teremos que:
Como se trata de uma mola do tipo engaste elástico, sabemos que a sua fórmula é dada por.
Sabemos que:
Substituindo teremos que: