Determine o deslocamento horizontal do ponto C do pórtico dado abaixo.
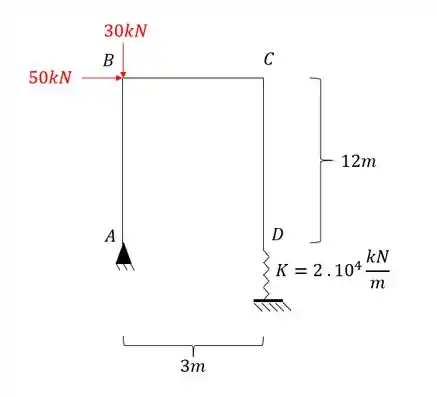
Passo 1
Sabemos que o que devemos fazer é determinar o sistema equivalente que iremos usar na nossa estrutura.
Como só temos uma mola vertical, teremos apenas apoios verticais, sendo assim o nosso sistema será dado por:
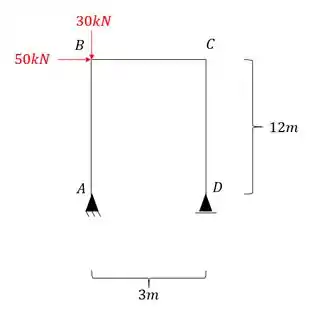
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
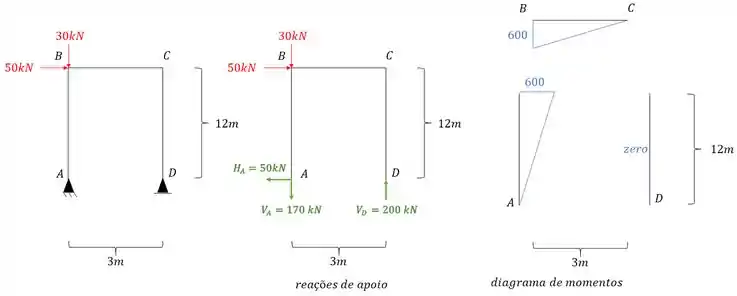
Passo 2
Agora precisamos determinar o deslocamento horizontal do ponto C.
- Deslocamento em C
Para descobrirmos o deslocamento horizontal nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
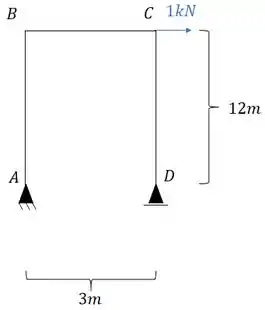
Agora nesse caso iremos ter um diagrama, e nesse caso o diagrama junto com as reações de apoio será dado por:
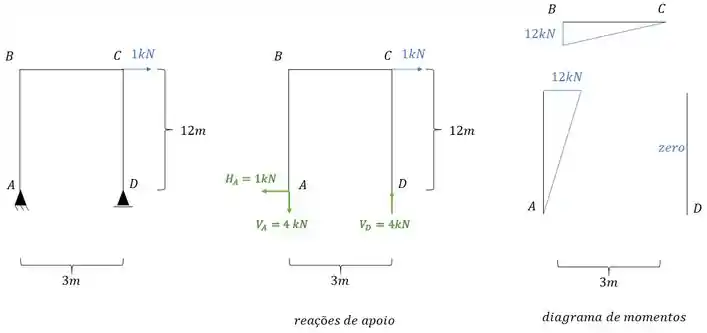
E devemos combinar ele com o diagrama de carregamentos reais que é dado por:
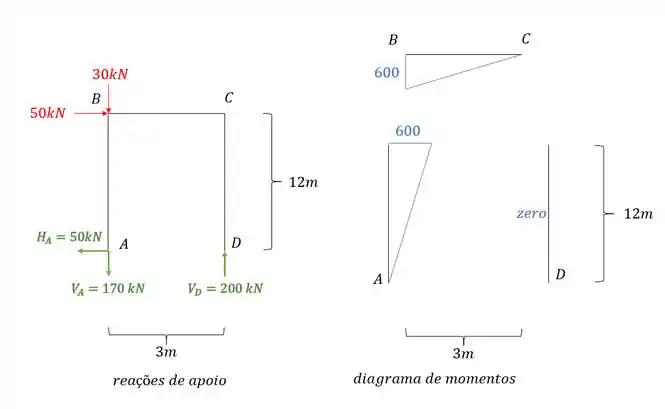
Combinando os diagramas teremos que:
Como temos que:
Substituindo teremos que:
Também temos as reações de apoio que serão dadas por.
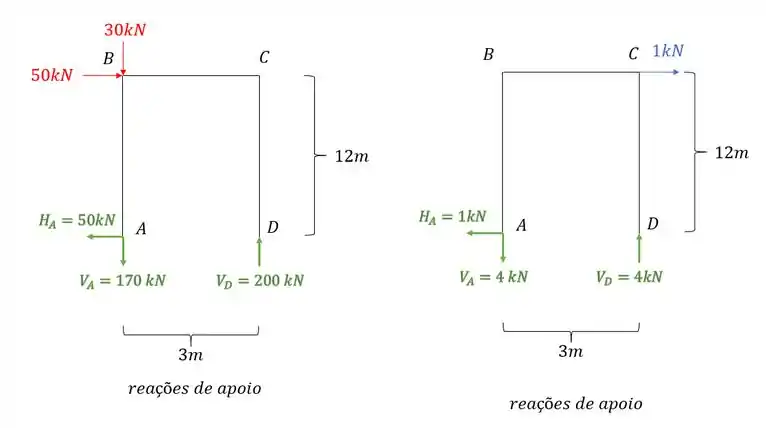
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
Substituindo o que temos na fórmula teremos que:
Logo a deformação total em C será a soma das duas parcelas dadas por: