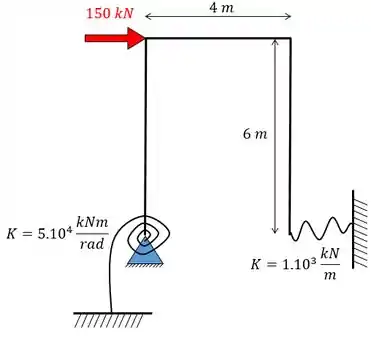
Determine as reações de apoio do pórtico abaixo.
Passo 1
Fala, galerinha!!! Esse problema pede para acharmos as reações de apoio e para isso é importante a gente perceber que existem dois apoios elásticos e que se trata de uma estrutura hiperestática.
Então a primeira coisa que vamos fazer é trocar os apoios elásticos por apoios simples. Depois nós vamos trabalhar apenas com a estrutura hiperestática, quebrando os apoios e aplicando as forças (hiperestáticos) correspondentes.
Por fim vamos aplicar o conceito dos deslocamentos para achar o hiperestático e o deslocamento pedido!
Passo 2
Vamos achar a estrutura correspondente, sem os apoios elásticos. A mola rotacional irá se transformar num engaste e a mola linear num apoio de primeiro gênero.
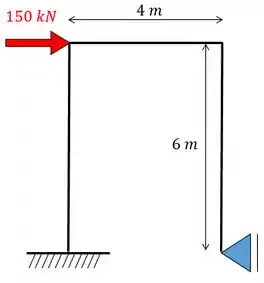
Perceba que temos uma estrutura hiperestática com grau hiperestático igual a 1. Então vamos quebrar um dos apoios de forma a obter um sistema isostático:
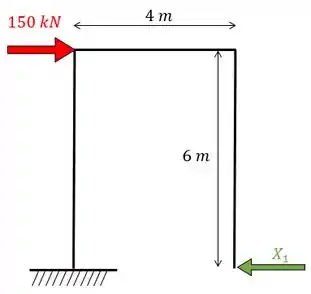
E como temos um hiperestático vamos dividir em 2 sistemas:
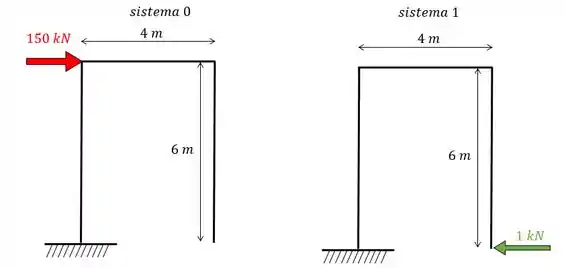
Passo 3
Beleza, agora vamos como vão ficar as nossas equações do deslocamento. Se não tivéssemos as molas a nossa equação seria da seguinte forma:
Mas a gente tem dois apoios elásticos que também irão se deslocar, então temos de aplicar o deslocamento referente aos apoios elásticos. Isso acontece da forma:
Ou seja, para cada e nós vamos ter na verdade três deslocamentos: o do sistema hiperestático, o da mola linear e o da mola rotacional. Assim vamos ter:
Onde:
Então para resolver nosso sistema nós vamos ter que achar esses 6 deltas ().
Passo 4
Vamos achar primeiro os deltas da estrutura hiperestática, e .
Para isso a gente precisa desenhar o diagrama do momento fletor para cada sistema, obtendo:
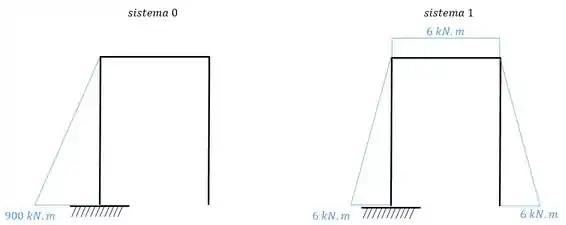
Agora vamos fazer as combinações, vamos começar com o deslocamento que, por ter duas barras com momento fletor nulo, nos fornece apenas a combinação de dois triângulos. Assim, vamos ter:
Substituindo os valores.
Esse já foi! Agora vamos para . Dessa vez vamos ter a combinação de (2 triângulos + 2 retângulos + 2 triângulos)
Substituindo os valores.
Para os sistemas hiperestáticos já acabamos agora vamos ver os deslocamentos referentes às molas.
Passo 5
No caso das molas nós vamos ter a linear e a rotacional sendo que para cada uma delas vamos aplicar as duas combinações dos sistemas e . Dessa forma podemos começar pela mola linear. Agora o que importa para nós não é o diagrama de momentos fletores mas sim as reações de cada apoio:
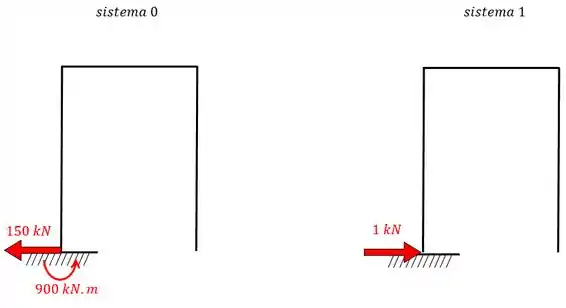
Aplicando a equação da mola linear vamos ter:
Substituindo os valores vamos obter:
E vamos fazer a mesma coisa para o sistema 11:
Substituindo os valores vamos obter:
Passo 6
Agora para a mola rotacional. No caso das molas lineares a gente utiliza as forças e para molas rotacionais utilizamos o momento. Lembrando do diagrama de resultantes:
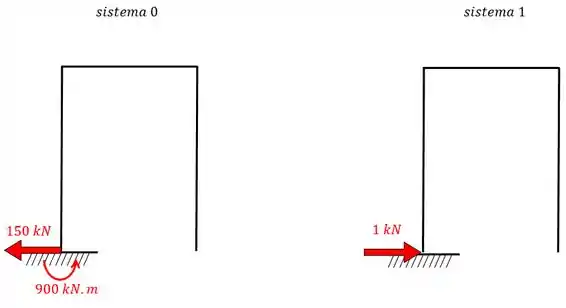
Aplicando o conceito:
Aqui não precisamos nem substituir porque no sistema 1 não há momento, logo . Dessa forma
Passo 7
Agora que achamos os 6 deltas vamos somar todos:
Obtendo:
Agora é só aplicar na equação real:
Passo 8
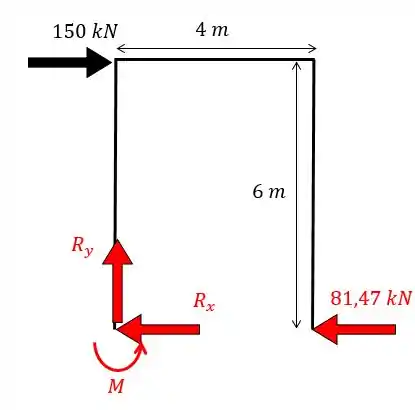
Agora é só achar o resto das forças:
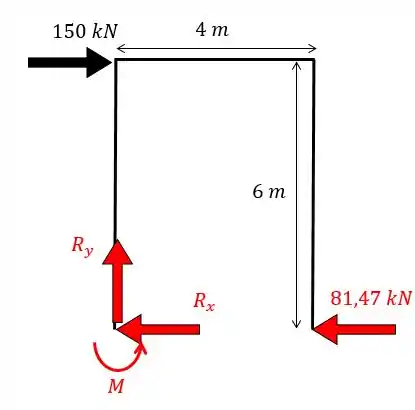
Aplicando as equações da estática vamos obter:
Resposta