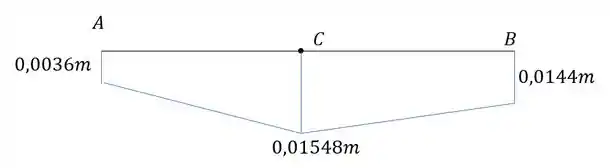
Determine o diagrama de deslocamentos verticais da viga dada abaixo, determinando pelo menos 3 pontos deslocados.
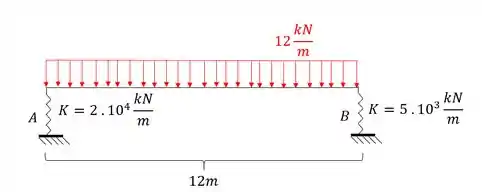
Passo 1
Antes de determinar qualquer coisa precisamos antes determinar os pontos que iremos determinar os deslocamentos, que nesse caso iremos usar estrategicamente os apoios e o ponto central da estrutura.
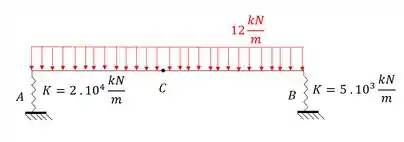
Passo 2
Em seguida sabemos que o que devemos fazer é determinar o sistema equivalente que iremos usar na nossa estrutura.
Como só temos molas verticais, teremos apenas apoios verticais, e como não temos forças horizontais, não iremos nós preocupar com o que ocorre na horizontal, sendo assim o nosso sistema será dado por:

Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
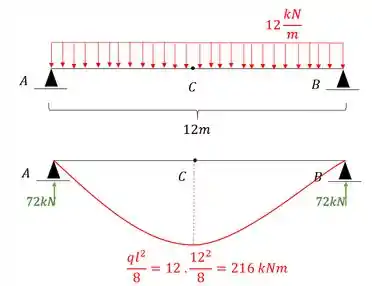
Passo 3
Agora precisamos descobrir o deslocamento de cada um dos pontos que tivermos definido. Perceba que como temos que descobrir os deslocamentos dos apoios, é melhor começarmos exatamente por eles, dessa maneira teremos que:
- Apoio em A
- Apoio em B
- Deformação em C
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
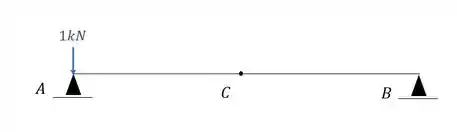
Perceba que esse diagrama será zero, logo, qualquer combinação entre diagrama será inútil para ver se tem deslocamento, pois já sabemos que nesse caso a combinação será zero.
Em contra partida temos as reações de apoio que serão dadas por.
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, é que nesse caso a reação em uma será zero, e por esse motivo será desprezada, mas substituindo o que temos na fórmula teremos que:
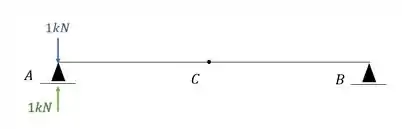
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:

Perceba que esse diagrama será zero, logo, qualquer combinação entre diagrama será inútil para ver se tem deslocamento, pois já sabemos que nesse caso a combinação será zero.
Em contra partida temos as reações de apoio que serão dadas por.
Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, é que nesse caso a reação em uma será zero, e por esse motivo será desprezada, mas substituindo o que temos na fórmula teremos que:
Passo 4
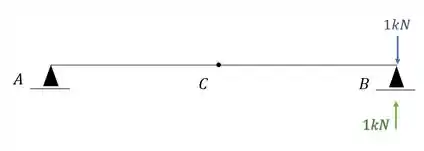
Para descobrirmos o deslocamento vertical nele, precisamos por uma carga unitária no ponto em que queremos saber e na direção que queremos saber, dessa maneira teremos que:
Agora nesse caso iremos ter sim diagrama, e nesse caso o diagrama junto com as reações de apoio será dado por:
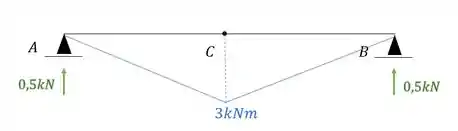
E devemos combinar ele com o diagrama de carregamentos reais que é dado por:
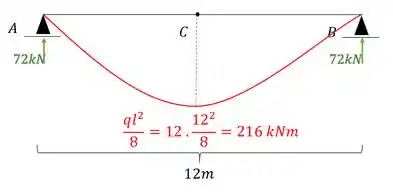
É usando a nossa tabela de combinações, sabemos que a combinação desses dois diagramas resulta em:
Também temos as reações de apoio que serão dadas por.

Porque a reação de apoio é importante para nós? Exatamente porque sabemos que a fórmula para determinar a deformação na mola é:
Sabemos que:
E perceba que consideramos a contribuição das duas molas, substituindo o que temos na fórmula teremos que:
Logo a deformação total em C será a soma das duas parcelas dadas por:
Tendo todas as deformações teremos que o nosso diagrama será:
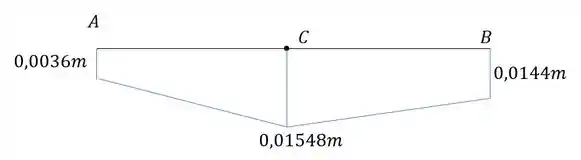
Resposta