Determine o diagrama de momentos fletores do pórtico abaixo.
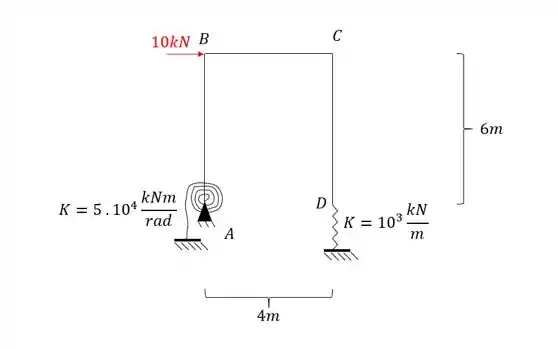
Passo 1
Antes de determinar qualquer coisa precisamos antes determinar o sistema equivalente que iremos usar na nossa estrutura.
No apoio esquerdo temos um apoio do segundo gênero, mas uma mola do tipo engaste elástico, sendo assim, podemos representar como um apoio do terceiro gênero. Em contra partida, o apoio da direita é apenas uma mola vertical, sendo dessa maneira apenas um apoio do primeiro gênero. Teremos assim que a nossa estrutura equivalente será:
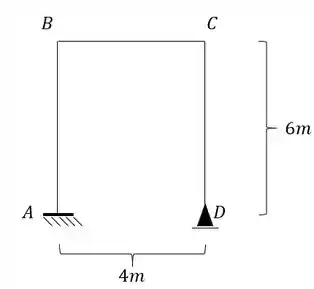
Perceba que nosso sistema equivalente é hiperestático, com 4 incógnitas e 3 equações. Com isso precisamos quebrar pelo menos um vínculo para termos um sistema isostático e dessa maneira resolvermos o seguinte sistema:
Passo 2
Quebrando o vínculo de momento do apoio engastado temos que:
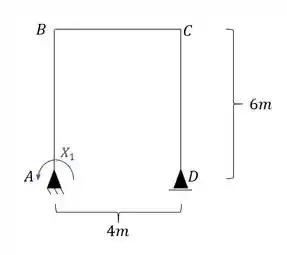
Sabemos que antes de começar a usar qualquer fórmula precisamos garantir logo o nosso diagrama para esse sistema equivalente com o carregamento externo, sendo assim, teremos que o nosso diagrama será:
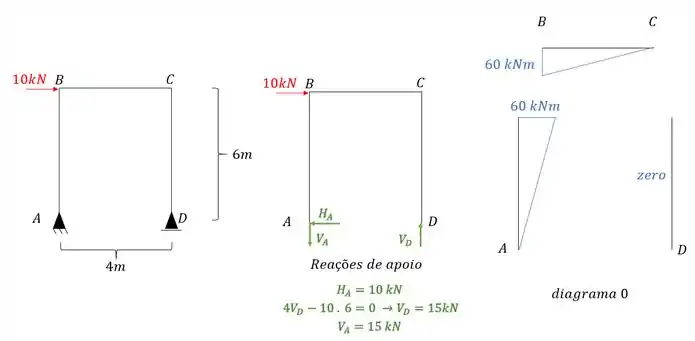
Passo 3
Da mesma maneira precisamos determinar o nosso diagrama considerando o nosso hiperestático igual a 1, sendo assim teremos que:
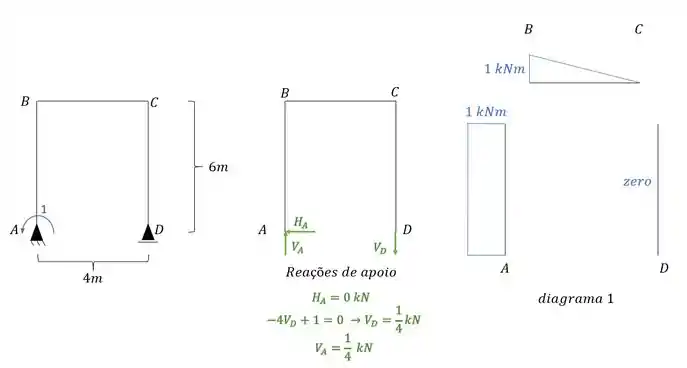
Passo 4
Agora precisamos determinar cada uma das nossas deformações, vamos começar pela deformação .
-
Sabemos que como temos mola na nossa estrutura deveremos tomar alguns cuidados, mas em suma, para nossa deformação devemos ter as seguintes parcelas:
- Combinação do diagrama zero com o diagrama 1
- Combinação da reação da mola em A no sistema zero e a reação da mola em A no sistema com a carga unitária (lembrando que que a mola em A é um engaste elástico)
- Combinação da reação da mola em D no sistema zero e a reação da mola em D no sistema com a carga unitária (lembrando que que a mola em D é uma mola vertical).
-
Sabemos que como temos mola na nossa estrutura devemos tomar alguns cuidados, mas em suma, para nossa deformação devemos ter as seguintes parcelas:
- Combinação do diagrama 1 com o diagrama 1
- Combinação da reação da mola em A no sistema com a carga unitária e a reação da mola em A no sistema com a carga unitária (lembrando que que a mola em A é um engaste elástico)
- Combinação da reação da mola em D no sistema com a carga unitária e a reação da mola em D no sistema com a carga unitária (lembrando que que a mola em D é uma mola vertical).
Sabendo disso vamos começar pela combinação de diagramas:
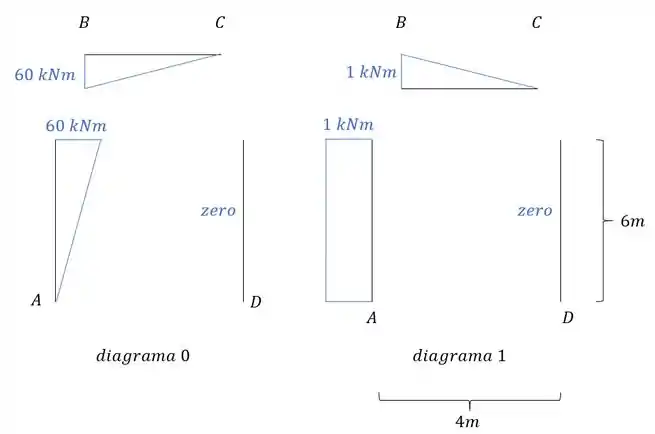
Precisamos fazer a combinação da mola que temos em A, e assim teremos que como é um engaste elástico a nossa fórmula será:
Olhando as reações de apoio teremos que:

Assim teremos que:
E por fim fazemos a combinação para determinação da contribuição da mola em B, que é uma mola vertical que calcularemos pela equação:
Olhando as nossas reações de apoio teremos que:

Substituindo teremos que:
Juntando tudo teremos que:
Passo 5
Agora precisamos determinar a deformação .
Sabendo disso vamos começar pela combinação de diagramas:
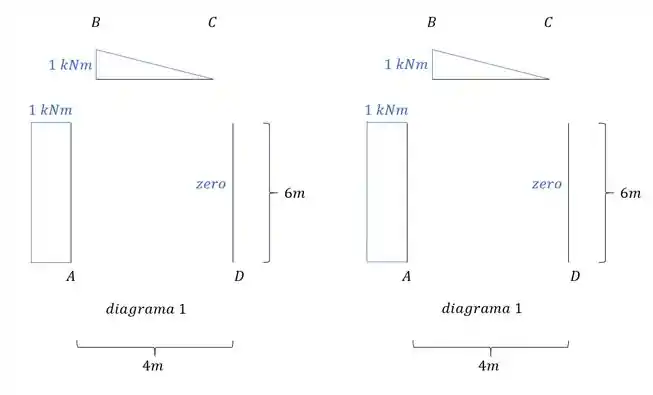
Precisamos fazer a combinação da mola que temos em A, e assim teremos que como é um engaste elástico a nossa fórmula será:
Olhando as reações de apoio teremos que:
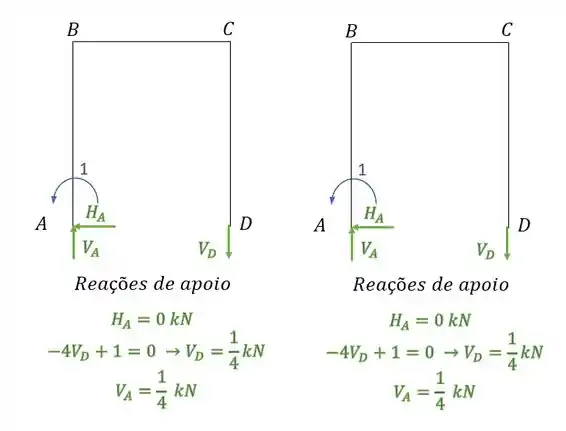
Assim teremos que:
E por fim fazemos a combinação para determinação da contribuição da mola em B, que é uma mola vertical que calcularemos pela equação:
Olhando as nossas reações de apoio teremos que:
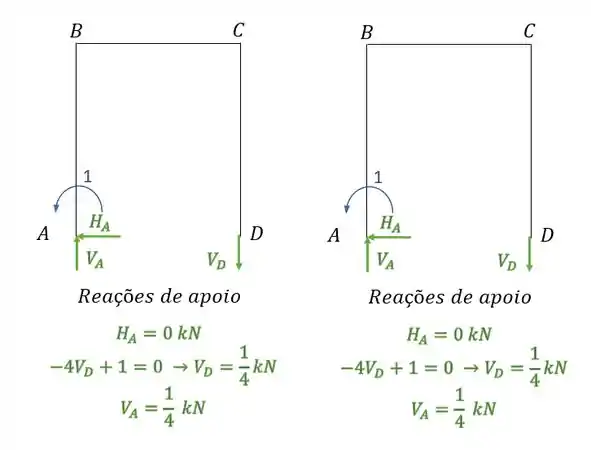
Substituindo teremos que:
Juntando tudo teremos que:
Passo 5
Agora substituímos no nosso sistema que é dado por:
Substituindo teremos que:
Passo 6
Para determinação dos momentos devemos usar:
Em que i é o ponto que estamos determinando o nosso momento, sendo assim teremos que:
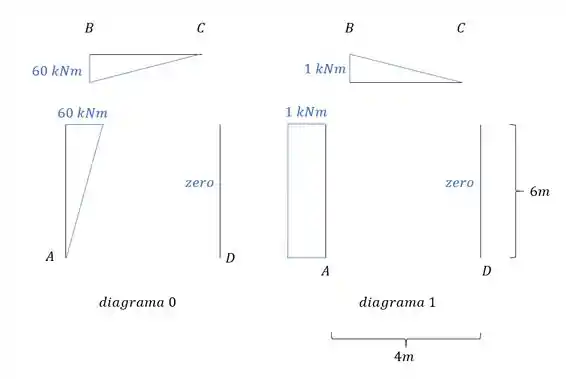
Substituindo vamos ter que:
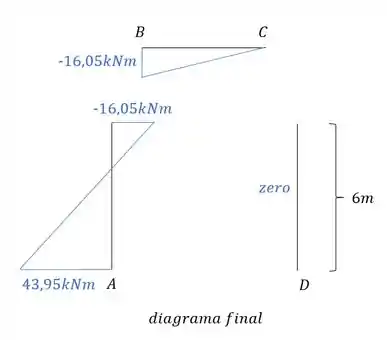
Montando esse diagrama vamos ter que:
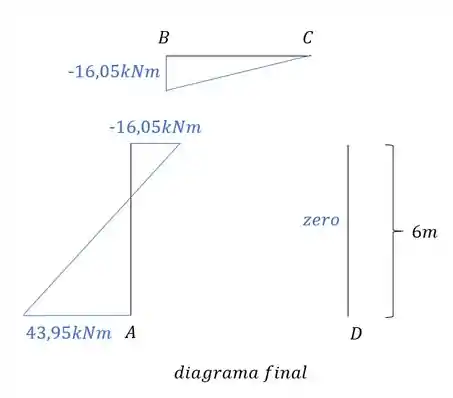
Resposta