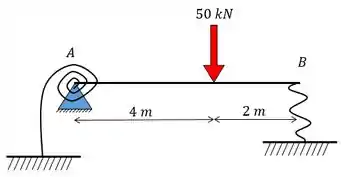
Calcule as reações nos apoios e da viga abaixo sabendo que a viga está apoiada por uma mola linear em e uma mola de rotação em . Dado: ; ;
Passo 1
Pessoal, vamos resolver essa questãozinha que tem uma viga em condição hiperestática e possui duas molas, como dito no enunciado. Uhullll
A primeira coisa que a gente tem que lembrar é que vamos retirar as molas e substituir por apoios fixos. Dessa forma a nossa resolução fica mais fácil pois resolvermos um problema hiperestático normal. Depois, lá no final do problema a gente calcula a parcela relativa aos apoios elásticos e soma tudo.
Vamos ver com calma tudo isso, partiu!
Passo 2
Vamos retirar as molas e substituí-las por outros tipos de apoio. Para isso a gente tem que lembrar que a mola de rotação é substituída por um apoio do tipo engaste ou carrinho. Como o apoio é de segundo gênero então vamos substituir por um engaste.
Já a mola linear será substituída por um apoio de primeiro gênero. Assim, vamos obter:
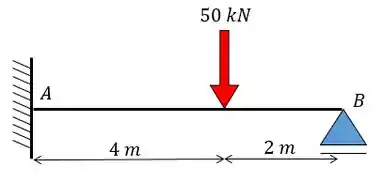
Pronto! Chegamos no nosso problema hiperestático convencional. Agora vamos resolvê-lo normalmente.
Passo 3
Este problema hiperestático possui um grau de hiperestaticidade, então vamos quebrar um vínculo (pode ser qualquer um, eu vou quebrar o apoio porque eu acho ele boboca) a gente só precisa lembrar que temos de colocar uma força equivalente. Dessa forma vamos obter:
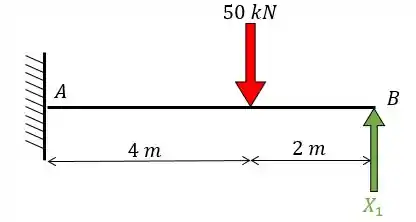
Eis que temos o nosso hiperestático e agora o que temos que fazer é achar o valor desse “indivíduo” escrutável... Para isso vamos dividir o problema em dois sistemas e fazer os seus respectivos diagramas de momento fletor.
Ps: Como, ao dividirmos o problema em dois sistemas, a gente obtém sistemas isostáticos, não vou perder muito tempo fazendo as contas não ok? Só vou mostrar como que fica o resultado para vocês =D
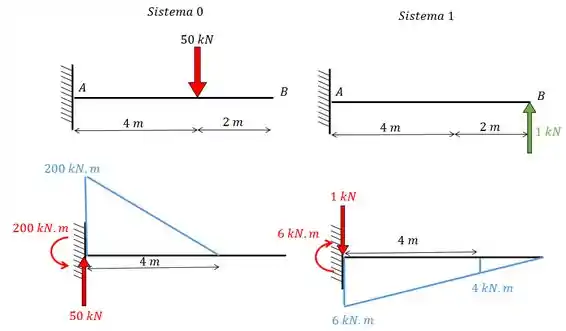
Viram como eu sou bonzinho e além de colocar o diagrama do momento fletor (em azul) ainda coloquei as forças resultantes (em vermelho). Owwnnnnn, que fofis....
Passo 4
Agora a gente tem que lembrar de como calcular o nosso hiperestático . A gente faz isso através da equação do deslocamento que tem a seguinte forma:
Então a gente vai precisar achar a deformação do sistema 0 em relação ao sistema 1 () e do sistema 1 em relação a ele mesmo (). Lembrando que vamos fazer isso com ajuda daquela nossa tabelinha marota.
Então vamos lá! Primeiro vamos calcular , aqui a gente precisa ficar ligado porque pode parecer que é a combinação de dois triângulos, mas na verdade é um triângulo e um trapézio. Isso acontece porque no sistema 0 o diagrama acaba em assim o triângulo do sistema 1 vira um trapézio =D
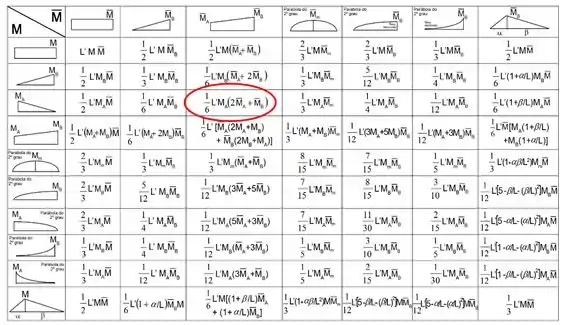
A tabela mostra a combinação de um triângulo com um trapézio:
Substituindo nós vamos ter:
Observe que há um sinal negativo que é introduzido devido aos sentidos opostos do momento fletor.
Agora para , dessa vez são dois triângulos mesmo:
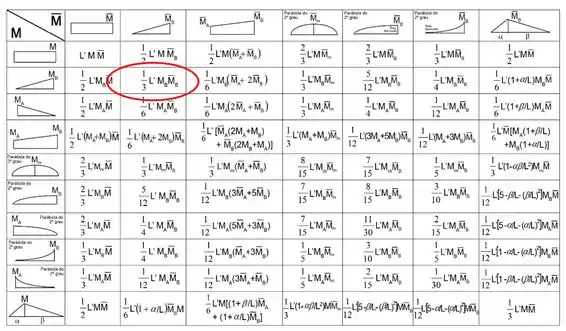
Pessoal, achamos os valores de e já podemos substituir na expressão abaixo?
A resposta é não =(
Por que a resposta é não? Porque se fizéssemos isso então a gente não estaria considerando a parte dos apoios elásticos, que até agora ainda não apareceram... Vamos ver como eles aparecem.
Passo 5
Para considerarmos a parte relativa aos apoios elásticos nós vamos calcular um novo e um novo , vamos chamá-los de e . Esses novos termos são as deformações de cada apoio elástico e são dados por aquelas equações que vimos na teoria:
Vamos olhar novamente as reações da nossa viga:
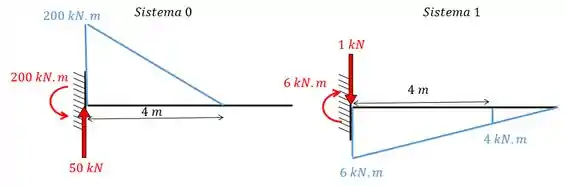
Com as reações vamos poder calcular os valores e .
Agora vamos fazer a substituição:
Para vamos ter:
Substituindo:
Passo 6
Agora podemos finalmente utilizar a equação para achar o nosso hiperestático . Para isso vamos somar os seguintes valores:
E vamos obter:
Obtendo.
E finalmente podemos substituir na equação do hiperestático:
Passo 7
Dessa forma vamos ter:
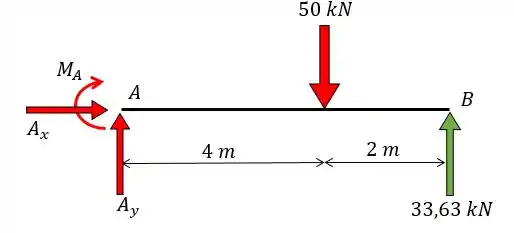
Nós achamos o nosso hiperestático que é
Pelas equações da estáticas vamos achar: