Um bocal é alimentado com de vapor d’água, a e a , e descarrega o fluido a e . Admitindo que a energia cinética do escoamento na seção de alimentação do bocal é pequena e que o processo é adiabático, determine a velocidade na seção de descarga do bocal e a área da seção de descarga do bocal.
Passo 1
O exercício pede para a gente calcular a velocidade da água saindo do bocal e a área do bocal por onde a água sai . A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
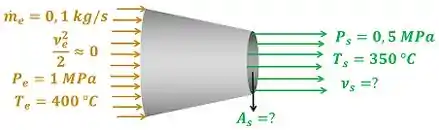
e são as velocidades da água entrando e saindo do bocal respectivamente. é a vazão mássica, é a pressão e é a temperatura do vapor d’água entrando no bocal. é a pressão e é a temperatura do vapor d’água saindo do bocal.
Agora que sabemos o que os dados significam, vamos aprender a calcular e .
Passo 2
é calculado a partir da primeira lei usada em um bocal em regime permanente. Como o enunciado diz que a energia cinética do escoamento na seção de alimentação do bocal é pequena, a gente considera que o termo .
e são as entalpias específicas da água entrando e saindo do bocal respectivamente.
Depois de encontrar esse valor para velocidade do vapor saindo do bocal , podemos encontrar a área pela qual esse vapor sai. Ela é calculada através da conservação de massa do bocal.
As fórmulas acima mostram que para calcular e , nós precisamos aprender a encontrar os valores de , e . Faremos isso no próximo passo!
Passo 3
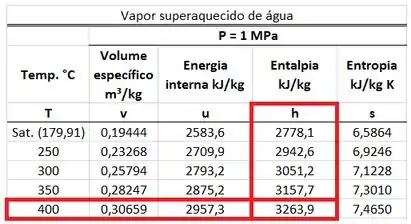
O valor de é achado na tabela de vapor superaquecido d’água para uma pressão de . Usamos a tabela de vapor superaquecido, porque a temperatura do vapor é maior que a temperatura de saturação . Ele está na mesma linha da temperatura de e na mesma coluna que a entalpia .
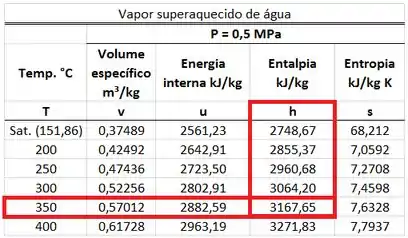
O valor de é achado na tabela de vapor superaquecido d’água para uma pressão de (esse valor é igual a ). Usamos a tabela de vapor superaquecido, porque a temperatura do vapor é maior que a temperatura de saturação . Ele está na mesma linha da temperatura de e na mesma coluna que a entalpia .
O valor de é calculado a partir do valor de pela fórmula abaixo.
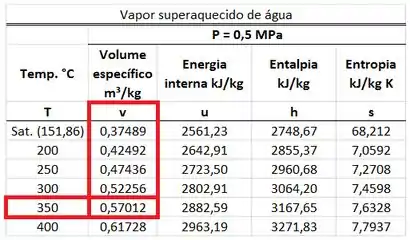
é achado na tabela de vapor superaquecido d’água para uma pressão de (esse valor é igual a ). Ele está na mesma linha da temperatura de e na mesma coluna que o volume específico .
Com esses valores em mãos, vamos iniciar as contas no próximo passo!
Passo 4
A fórmula de já foi criada na etapa acima. No entanto, para a gente conseguir usar essa fórmula corretamente, precisamos converter os valores de e de para .
Substituindo esses valores na fórmula, encontramos:
Antes de achar , precisamos calcular .
Enfim, temos tudo para determinar .