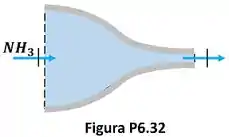
A Fig. P6.32 mostra o esquema de um bocal isolado que é alimentado com vapor de amônia ( e ). A velocidade do escoamento na seção de entrada do bocal é baixa. A pressão e a velocidade, na seção de saída, são respectivamente iguais a e . Sabendo que a vazão em massa no bocal é , calcule a temperatura e o título, se aplicável, da amônia na seção de saída do bocal e a área da seção de descarga do bocal.
Passo 1
O exercício pede para a gente calcular a temperatura e o título da amônia saindo do bocal. Além disso, ele pede para a gente determinar o valor da área de descarga do bocal . A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.
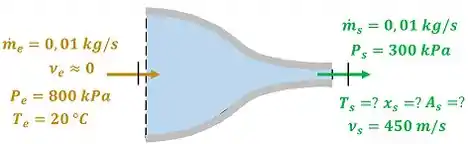
e são as velocidades da amônia entrando e saindo do bocal respectivamente. e são as vazões mássicas da amônia entrando e saindo do bocal! é a pressão e é a temperatura do vapor de amônia entrando no bocal. é a pressão da amônia saindo do bocal.

Agora que sabemos o que os dados significam, vamos entender as etapas que temos que seguir para calcular , (caso a amônia saindo do bocal esteja saturada) e .
Passo 2
- Aprender a calcular o valor da entalpia da amônia que está saindo do bocal. Para isso, usaremos a primeira lei da termodinâmica.
- Aprender a saber se a amônia é um vapor superaquecido ou uma mistura saturada ou um líquido comprimido.
- Aprender a calcular o título da amônia a partir do valor de .
- Aprender a encontrar os valores das entalpias que serão mostradas mais tarde (, , ) e da massa específica da amônia saindo do bocal .
- Fazer as contas!
Passo 3
é calculado a partir da primeira lei usada em um bocal em regime permanente. Como o enunciado diz que é pequena, a gente considera que o termo .
Se for maior que a entalpia específica do vapor saturado a , a amônia está na forma de vapor superaquecido.
Se for menor que a entalpia específica do líquido saturado a , a amônia está na forma de líquido comprimido.
Se for maior que a entalpia específica do líquido saturado a e menor que a entalpia específica do vapor saturado a , a amônia está saturada.
Se a amônia for saturada, o título pode ser calculado pela fórmula abaixo.
Além disso, a temperatura da amônia será igual à temperatura de saturação a .
Depois de encontrar esse valor, podemos encontrar a área pela qual a amônia sai. Ela é calculada através da conservação de massa do bocal.
As fórmulas acima mostram que para calcular , e , nós precisamos aprender a encontrar os valores de , , e . Faremos isso nos próximos passos!
Passo 4
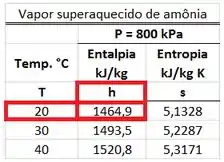
é determinado através da tabela de vapor superaquecido de amônia a . O valor de está na mesma linha que a temperatura de e na mesma coluna que a entalpia .
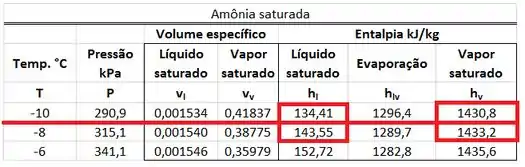
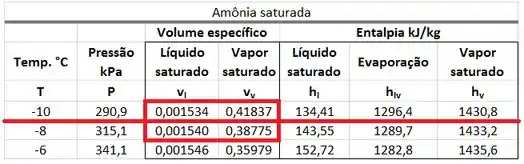
Os valores de e são achados na tabela de saturação de amônia para uma pressão de . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado . está na mesma linha da pressão de e na mesma coluna que a entalpia do líquido saturado .
Como a pressão de não se encontra nessa tabela, teremos que interpolar os valores de e usando os valores de e das pressões de e .
Passo 5
O valor de é calculado a partir do valor de pela fórmula abaixo.
é achado na tabela de saturação de amônia para uma pressão de . Se a amônia da saída estiver saturada, o valor de vai depender do volume específico do líquido saturado a e do volume epecífico do vapor saturado a . A fórmula de se encontra abaixo.
está na mesma linha da pressão de e na mesma coluna que o volume específico . está na mesma linha da pressão de e na mesma coluna que o volume específico . Como a pressão de não se encontra nessa tabela, teremos que interpolar os valores de e usando os valores de e das pressões de e .
Com esses valores em mãos, vamos iniciar as contas no próximo passo!
Passo 6
Primeiro, precisamos calcular . Para calcular nós precisamos dividir o termo de energia cinética por mil para passa esse termo de para .
Esse valor de está entre e . Portanto, a amônia saindo do bocal está saturada e tem um título . O cálculo de se encontra abaixo.
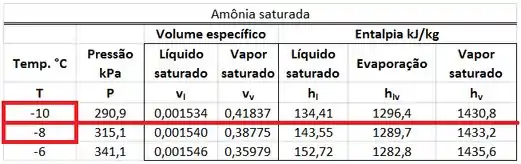
Como a amônia está saturada, o valor da sua temperatura é o valor da temperatura de saturação para de pressão. Como não existe uma linha na tabela com essa pressão, teremos que interpolar o valor de usando os valores de das pressões de e .
Passo 7
Antes de achar , precisamos calcular .
Com isso, achamos .
Enfim, temos tudo para determinar .