Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Bocais e Difusores

Ver Teoria
Exercício 31245678

Enunciado

A parte frontal de um turbina de avião atua como um difusor. O escoamento de ar na seção de alimentação deste difusor apresenta velocidade igual a 900   k m / h , T = - 5   ° C e P = 50   k P a . A velocidade na seção de alimentação do compressor, que está montado a jusante deste difusor, é 80   m / s . Sabendo que a relação entre as áreas do compressor e do difusor é igual a 0,8 , determine a temperatura e a pressão na seção de alimentação do compressor.

Passo 1

O exercício pede para a gente calcular a temperatura T s e a pressão P s do ar saindo do difusor e entrando no compressor. Mas cuidado! Não confunda! O exercício é só de difusor, não de compressor.

No entanto, a saída do difusor está conectada à entreda do compressor e isso muda a questão em relação à exercícios comuns de difusor! Isso significa que essa saída do difusor é obstruída por outro equipamento. Logo, o ar não terá tanto espaço pra passar! Isso vai fazer com que a área de saída do ar seja menor que a área de entrada no difusor! Essa novidade desse exercício pode te fazer ficar com dúvida, porque, no caso de um difusor sozinho, a sua área de sapida é maior que a área de entrada!

A figura baixo mostra todos os dados fornecidos pelo enunciado para calcular esses valores.

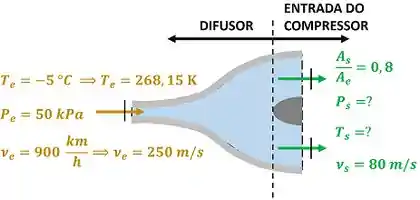
ν e e ν s são as velocidades do ar entrando e saindo do difusor respectivamente. A e e A s são as áreas das seções de alimentação e descarga do difusor! P e é a pressão e T e é a temperatura do ar entrando no difusor.

Agora que sabemos o que os dados significam, vamos entender as etapas que temos que seguir para calcular T s e P s .

Passo 2

  1. Calcular o volume específico v e do ar entrando no difusor através da fórmula de gases perfeitos.

    2. P e ⋅ v e = R a r ⋅ T e       ⟹       v e = R a r ⋅ T e P e

    onde R a r é a constante de gás do ar que vale 0,2870   k J / k g ⋅ K .

  2. Calcular o volume específico v s do ar saindo do difusor através da fórmula de conservação de massa.

    3. m ˙ s = m ˙ e

    ρ s ⋅ A s ⋅ ν s = ρ e ⋅ A e ⋅ ν e

    A s ⋅ ν s v s = A e ⋅ ν e v e

    v s = A s A e ⋅ ν s ⋅ v e ν e

  3. Calcular T s a partir da primeira lei da termodinâmica aplicada ao difusor e considerando que o calor específico c P 0 é constante e vale 1,0035   k J / k g ⋅ K .

    4. h e + ν e 2 2 = h s + ν s 2 2     ⟹     h s - h e = ν e 2 2 - ν s 2 2       ⟹       c P 0 ⋅ T s - T e = ν e 2 2 - ν s 2 2

    T s = 1 c P 0 ⋅ ν e 2 2 - ν s 2 2 + T e

    Para usar esse valor na fórmula, temos que nos lembrar de converter de k J k g ⋅ K para J k g ⋅ K .

    c P 0 = 1,0035   k J k g ⋅ K       ⟹       c P 0 = 1003,5   k J k g ⋅ K

  4. Calcular P s , lembrando que o número de k m o l de ar que entra no difusor ( n e ) é igual ao número de k m o l de ar que sai do difusor n s , porque o ar está escoando em regime permanente. Logo, tudo que entra tem que sair.

n e ⋅ R a r = n s ⋅ R a r       ⟹     P e ⋅ v e T e = P s ⋅ v s T s       ⟹       P s = P e ⋅ v e ⋅ T s v s ⋅ T e

Passo 3

Agora que temos o passo a passo, vamos iniciar as contas!

v e = R a r ⋅ T e P e       ⟹     v e = 0,2870 ⋅ 268,15 5 0       ⟹       v e = 1,539   m 3 k g

v s = A s A e ⋅ ν s ⋅ v e ν e       ⟹     v s = 0,8 ⋅ 8 0 ⋅ 1,539 25 0       ⟹       v s = 0,394   m 3 k g

T s = 1 c P 0 ⋅ ν e 2 2 - ν s 2 2 + T e

T s = 1 1003,5 ⋅ 25 0 2 2 - 8 0 2 2 + 268,15       ⟹       T s = 296 , 1   K

P s = P e ⋅ v e ⋅ T s v s ⋅ T e       ⟹       P s = 5 0 ⋅ 1,539 ⋅ 296 , 1 0,394 ⋅ 268,15       ⟹       P s = 215,7   k P a

Resposta

T s = 296 , 1   K

P s = 215,7   k P a

Exercícios de Livros Relacionados

O bocal de propulsão de um motor a jato é alimentado com ar a 1000K e 200k P a . Sabendo que a velocidade do ar na seção de alimentação do bocal é 30m / s , que o ar é descarregado do bocal a 850K e 9
6- O jato de água líquida, a 15° C , descarregado de um bocal atinge a altura de 15m . Qual é a velocidade do escoamento na seção de descarga do bocal?
Um difusor é alimentado com ar a 300K e 100k P a . Sabendo que a velocidade na seção de alimentação do difusor é igual a 300m / s , que a velocidade na seção de descarga é muito baixa e que o escoamen
Um bocal convergente é alimentado com nitrogênio a 200k P a e 400K . O escoamento na seção de descarga do bocal apresenta temperatura e pressão iguais a 330 K e 100k P a . Sabendo que a velocidade do
Um difusor é alimentado com um escoamento de gás perfeito que apresenta velocidade igual a 250m / s , T = 300K e p = 100k P a . A velocidade do escoamento na seção de descarga do difusor é 25m / s . D