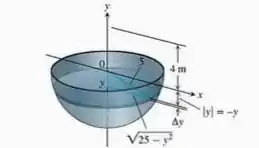
Descrevemos o bombeamento do conteúdo de recipientes esféricos da mesma maneira que fazemos com outros reservatórios, com o eixo de integração ao longo do eixo vertical da esfera. Considere a figura a seguir e determine quanto trabalho será necessário para que um reservatório hemisférico, de raio , cheio de água, seja esvaziado ao se bombear seu conteúdo até uma altura acima do topo do reservatório. O peso específico da água é .
Passo 1
Novamente, temos um problema de bombeamento. De novo, vamos fazer a suposição de que a força realizada é suficiente apenas para bombear o líquido a uma velocidade constante, ou seja, nesse caso, a força de bombeamento é igual ao peso do líquido:
Essa força é realizada ao longo do eixo . A linha da altura de atuação do bombeamento vai da altura máxima, , até o nível de água, que se encontra numa “altura negativa” , uma vez que o hemisfério da esfera está na parte negativa do eixo . Assim, temos que a distância que a força atua é definida como . Logo:
Passo 2
O mais difícil nessa caso é achar uma uma expressão para em função de, nossa variável de integração. O peso do líquido é dado por:
Agora, observa que o volume varia ao longo do eixo , porque a área da seção transversal vai mudando. A forma de resolver isso é escrever o volume em sua forma infinitesimal. Para isso, vamos pensar em cada fatia infinitesimal de líquido. Nesse caso, temos:
O raio equivale ao valor de para cada fatia infinitesimal, então podemos escrever:
A relação entre e foi dada na figura:
Logo, podemos reescrever:
Sabemos que
Logo, em função de :
Sabendo que:
E os limites de integração?
Pelo desenho dado, a água é bombeada de até , concorda? Ele próprio colocou os eixos na figura, então eu tenho que entender o desenho!
Substituindo:
Pronto! Agora tudo dentro da integral está em função de , nossa variável de integração. Todo o resto são constantes.
- ''Passo 3
Resolvendo a integral:
No enunciado, ele dá o peso específico da água. O peso específico de um líquido é definido como:
Logo, temos:
Substituindo: