O tanque abaixo tem o formato de um tronco de cone e está cheio de um liquido de densidade . O raio da base maior é de metros, o raio da base menor é de metros e a altura é de metros. O tanque está apoiado sobre a base menor. Considere a aceleração da gravidade.
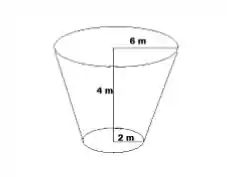
Encontre o trabalho necessário para bombear todo o liquido pela saída, que se encontra na parte superior do tanque.
Passo 1
Bom, temos um problema de bombeamento. A primeira coisa que fazemos ao ver um problema como esse é identificar quem é a força, que é o que vai entrar na integral. Ele não deixa isso claro no enunciado, mas aí nós fazemos uma suposição aqui: consideramos que a força realizada é suficiente apenas para bombear o líquido a uma velocidade constante, ou seja, nesse caso, a força de bombeamento é igual ao peso do líquido:
Essa força é realizada ao longo do eixo . Mas qual a distância em que a força atua? A distância em que ela puxa o líquido é de , altura de subida do líquido. Essa é a distância em que a força atua. Então podemos escrever:
Passo 2
O mais difícil nessa caso é achar uma uma expressão para em função de, nossa variável de integração. O peso do líquido é dado por:
Agora, observa que o volume varia ao longo do eixo , porque a área da seção transversal vai mudando. A forma de resolver isso é escrever o volume em sua forma infinitesimal. Para isso, vamos pensar em cada fatia infinitesimal de líquido. Nesse caso, temos:
O raio equivale ao valor de para cada fatia infinitesimal, então podemos escrever:
A relação entre e pode ser encontrada vendo o quanto o raio aumenta quando caminha a sua altura inteira:
De onde sai que,
Logo, podemos reescrever:
Passo 3
Sabemos que
Logo, em função de :
Sabendo que:
Substituindo:
Onde os limites de integração vieram do inicial e final do fluido.
Pronto! Agora tudo dentro da integral está em função de , nossa variável de integração. Todo o resto são constantes.
Passo 4
Resolvendo a integral:
O enunciado nos disse que a densidade vale e a gravidade vale . Logo,