Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Bombeamento

Ver Teoria
Exercício 4123

Enunciado

Cálculo de Volumes através de Integrais

Seja S a superfície gerada pela rotação da elipse x 2 4 + y 2 = 1 em torno do eixo y . Considere um reservatório de água no formato de S cheio até a metade( x e y medidos em metros). Qual o trabalho para bombear toda a água, que deve sair por uma abertura no topo do reservatório? Deixe sua resposta em termos de g e μ , a aceleração da gravidade e a densidade da água, respectivamente.

Passo 1

Bom, primeira coisa a se fazer é entender o enunciado. O cara te falou que ele vai encher um volume S de água, e quer saber qual o trabalho pra bombear a água pra cima, de forma que ela saia pela abertura no topo. Então, um bom começo é identificar qual é o volume S , ou seja, qual a quantidade de água que vamos ter que bombear.

A superfície S vai ser um “ovo”, mais ou menos assim:

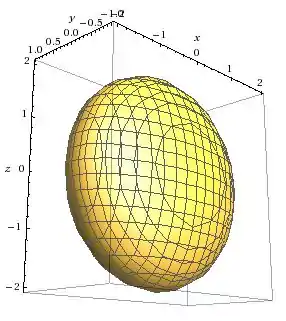
E imaginem que a gente corte esse ovo em várias fatias de espessura d y . Vamos poder dizer que cada fatia dessa tem um volume d V = π R 2 d y . Aonde esse R que apareceu aí é o raio de cada minifatia que a gente tiver do ovo. E se vocês repararem bem, esse raio é exatamente o valor de x correspondente a cada fatia. Como a nossa equação diz que:

x 2 4 + y 2 = 1

Então:

x 2 = 4 1 - y 2

Como o raio R é igual a x , podemos escrever que:

d V = 4 π 1 - y 2 d y

Passo 2

Até agora, escrevemos o volume de água de cada fatia do ovo que temos pra bombear. Agora podemos escrever que a massa de água de cada fatia que vamos bombear é:

m = μ d V = μ 4 π 1 - y 2 d y

Feito isso, vamos interpretar o enunciado: Se ele quer bombear a água pra cima, de forma que ela saia na abertura em cima do reservatório, significa que a força F que devemos aplicar na água é F = m g .

Passo 3

Então vamos finalmente chegar no que o problema pediu: TRABALHO!

Vamos lembrar que o trabalho realizado na água será W = F d = m g d , e o deslocamento d , que a água vai ter que percorrer até chegar na abertura em cima, vai ser o d = y m á x - y = 1 - y , porque o ponto mais alto do ovo acontece quando y = 1 = y m á x .

Passo 4

Finalmente juntando tudo que nós escrevemos até agora, e somando o trabalho realizado pra bombear cada fatia de água do ovo, vamos ficar com a seguinte expressão:

W = ∫ 4 μ g π 1 - y 2 1 - y d y

E como o reservatório está cheio SOMENTE até a metade, o intervalo de integração vai ser - 1 < y < 0 .

Então, olha que integral bonita pra resolver:

W = ∫ - 1 0 4 μ g π 1 - y 2 1 - y d y

Passo 5

Resolvendo a integral:

W = 4 μ g π ∫ - 1 0 ( 1 - y - y 2 + y 3 ) d y

W = 4 μ g π 0 - - 1 - 1 2 + 1 3 + 1 4

W = 4 μ g π 11 12 = 11 μ g π 3   J →

Resposta

W = 11 μ g π 3   J →

Exercícios de Livros Relacionados

Resolva o Exercício 22 se o tanque estiver cheio até a metade de óleo, que tem densidade de 900 kg/m³.
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =y 2 ; x = - y ; y = 2 ; y0
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =2 y - y 2 ; x = 0
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: y = x ; y = 0 ; y = x - 2