Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 27

27. Prove que no método de Gauss-Seidel vale a relação:

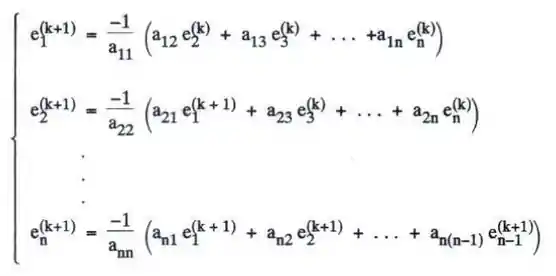
Passo 1

a) E ai meu bom!

Se liga só! O método de Gauss-Seidel faz a partição da matriz dos coeficientes  A  em  L  (estrita matriz triangular inferior),  D (matriz diagonal) e  U  (estrita matriz triangular superior), de acordo com Venkateshan e Swaminathan.

Isso significa que a matriz dos coeficientes é o resultado da soma das matrizes:

A = L + D + U

Então, temos que:

L + D + U x = b

Passo 2

No processo iterativo, a ( k + 1 ) -ésima iteração é baseada no resultado da ( k ) -ésima iteração. A inversa de uma matriz diagonal é simplesmente o valor recíproco do elemento da diagonal principal. O sistema de equações pode ser escrito como:

x i k + 1 = b i - ∑ j = 1 i - 1 a i j x i j k - ∑ j = i + 1 n a i j x j k a i i

Quanto ao cálculo do erro, consiste em se pegar a maior diferença entre as raízes da iteração k - 1 e k , e dividi-las por o valor de x máximo da iteração atual...

e k = max ⁡ | x i k - x i k + 1   | max 1 ≤ i ≤ n ⁡ | x i k |

Passo 3

Sendo assim, fazendo as iterações, para a primeira, obtemos que...

e 1 k + 1 = - 1 a 11 a 12 e 2 k + a 13 e 3 k + … + a 1 n e n k

Para a segunda, temos que...

e 2 k + 1 = - 1 a 22 a 21 e 2 k + 1 + a 2 3 e 3 k + … + a 2 n e n k

E para a n -ésima iteração...

e n k + 1 = - 1 a n n a n 1 e 2 k + 1 + a n 3 e 3 k + 1 + … + a n n e n k + 1

Chegando então, a relação proposta pelo enunciado...

e 1 k + 1 = - 1 a 11 a 12 e 2 k + a 13 e 3 k + … + a 1 n e n k e 2 k + 1 = - 1 a 22 a 21 e 2 k + 1 + a 23 e 3 k + … + a 2 n e n k ⋮ e n k + 1 = - 1 a n n a n 1 e 2 k + 1 + a n 3 e 3 k + 1 + … + a n n e n k + 1

Resposta

e 1 k + 1 = - 1 a 11 a 12 e 2 k + a 13 e 3 k + … + a 1 n e n k e 2 k + 1 = - 1 a 22 a 21 e 2 k + 1 + a 23 e 3 k + … + a 2 n e n k ⋮ e n k + 1 = - 1 a n n a n 1 e 2 k + 1 + a n 3 e 3 k + 1 + … + a n n e n k + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada caso: verifique se o critério de Sassenfeld é satisfeito ;resolva por Gauss-Seidel , se possível: A = 4 - 1 0 0 - 1 4 - 1 0 0 - 1 4 - 1 0 0 - 1 4 ; b = 1 1 1 1
Considere o sistema linear: 1 2 1 2 3 1 3 5 2 x 1 x 2 x 3 = 3 5 1 Verifique, usando eliminação gaussiana que este sistema não tem solução. Qual será o comportamento usando Gauss Seidel?Através de um s
Em cada caso: verifique se o critério de Sassenfeld é satisfeito ;resolva por Gauss-Seidel , se possível: A = 10 1 1 1 10 1 1 1 10 ; b = 12 12 12
Usando o critério de Sassenfeld, verifique para que valores positivos de k se tem garantia de que o método de Gauss-Seidel vai gerar uma sequência convergente para a solução do sistema: k x 1 + 3 x 2