Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 3
3. Verifique que o número de operações necessárias no método de Eliminação de Gauss, sem pivoteamento parcial, é , na fase de triangularização da matriz A, e , na fase de resolução do sistema triangular superior. Estão sendo contadas as operações de divisão, multiplicação e soma.
Lembrando que
Passo 1
O objetivo do método de Gauss consiste em eliminar os elementos de forma a obter um sistema equivalente com uma matriz triangular superior. Tendo uma matriz triangular, basta aplicar substituições sucessivas para chegarmos à solução pretendida.
O método consiste em passos, onde construímos elementos a partir dos elementos considerando como a matriz inicial.
Desse modo, para um passo , com indo de até ...
- Se o pivô então é preciso efetuar a troca de linha.
- Já se , temos o exposto na seguinte imagem abaixo:
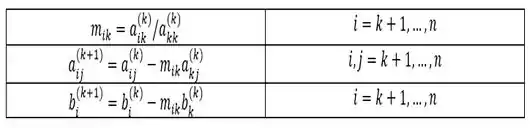
Passo 2
No final dos passos, obtemos o sistema triangular superior equivalente:
Cuja resolução é dada através de substituição ascendente...
E obtemos então, que...
Passo 3
Agora, vamos ver qual o número de operações envolvido na resolução de um sistema
Na fase de triangularização da matriz A para cada passo , temos um total de divisões, o que corresponde a um total de...
E calculando os , temos um total de multiplicações e subtrações, o que corresponde a um total de...
Quanto ao cálculo de , para cada passo , temos multiplicações e subtrações, o que nos faz chegar à...
Sendo assim, no total temos que...
E também...
E então, chegamos ao número de operações proposta pelo enunciado, que é dada por...