Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 24

Considere o sistema linear:

Verifique, usando eliminação gaussiana que este sistema não tem solução. Qual será o comportamento usando Gauss Seidel?

Através de um sistema 2X2 , dê uma interpretação geométrica do que ocorre com Gauss-Seidel quando o sistema não tem solução e quando tem infinitas soluções.

Passo 1

Fala galerinha, tudo certinho?

Vamos começar transformando a matriz em uma matriz para resolver por Gauss:

Podemos fazer :

Se fizermos

Dessa forma, nosso sistema ficaria assim:

Como , esse sistema não tem solução!

Passo 2

Em um sistema sem solução vamos ficar fazendo iterações pra sempre sem nunca chegar num resultado. E em um sistema com infinitas soluções teremos um resultado na primeira iteração haha

Sistema com infinitas soluções:

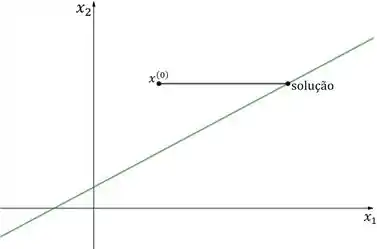
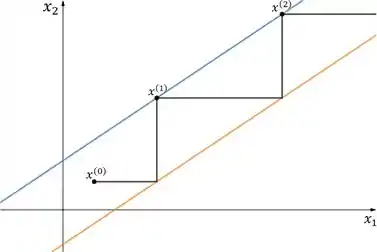
Sistema sem solução:

Resposta

Gauss: sem solução

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada caso: verifique se o critério de Sassenfeld é satisfeito ;resolva por Gauss-Seidel , se possível: A = 4 - 1 0 0 - 1 4 - 1 0 0 - 1 4 - 1 0 0 - 1 4 ; b = 1 1 1 1

Em cada caso: verifique se o critério de Sassenfeld é satisfeito ;resolva por Gauss-Seidel , se possível: A = 10 1 1 1 10 1 1 1 10 ; b = 12 12 12

Usando o critério de Sassenfeld, verifique para que valores positivos de k se tem garantia de que o método de Gauss-Seidel vai gerar uma sequência convergente para a solução do sistema: k x 1 + 3 x 2

29. Considere o sistema linear cuja matriz dos coeficientes é a matriz esparsa.a) Ache a solução por inspeçãob) Faça mudanças de linhas na matriz original para facilitar a aplicação do método da elimi