Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 36
36. Dizemos que : é uma matriz banda com amplitude se quando .
Escreva um algoritmo para obter a fatoração de Cholesky de uma matriz banda , simétrica, definida positiva, tirando proveito de sua estrutura.
Passo 1
E ai meu bom!
Se liga só! O algoritmo para a fatoração de Cholesky necessita cerca de metade do espaço requerido pela decomposição , por conta da simetria, e cerca de metade dos flops de , . Isso pode ser feito porque os cálculos podem ser feitos elemento a elemento.
Dizemos que é uma matriz banda se existem inteiros e , com , , tais que...
O valor é chamado tamanho da banda. Além disso, p é chamado tamanho da banda inferior e q é o tamanho da banda superior.
Passo 2
Sendo assim, com base no seguinte algoritmo pra resolver esse tipo de problema, em pseudocódigo...
Através da linguagem Java, obtemos que...
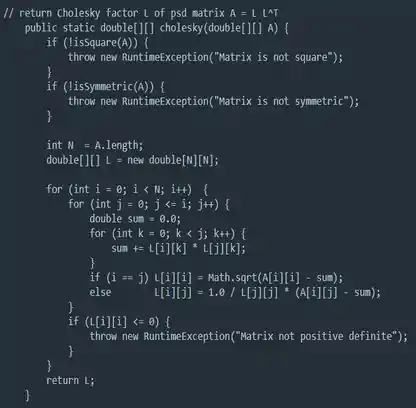
Resposta
Ei, a resposta está no passo a passo :)