Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 2

Ajuste os dados abaixo pelo método dos quadrados mínimos utilizando:

  1. Um reta
  2. Uma parábola do tipo a x 2 + b x + c

Trace as duas curvas no gráfico de dispersão dos dados. Como você compararia as duas curvas com relação aos dados?

Passo 1

Fala galerinha, tudo certinho?

Bom, esse exercício é para aplicarmos a ferramenta do método dos mínimos quadrados, o exercício pede pra fazermos dois tipos de aproximações : a linear e a parábola.

Onde usaremos alguns tipos de fórmulas que precisamos aplicar para encontrar as fórmulas q eu mais se aproximam do valor real.

Quando fizermos a aproximação linear, teremos:

φ x k = a 0 + a 1 x k

E para isso usaremos:

a 0 m + a 1 ∑ k = 1 m x k = ∑ k = 1 m y k

E também:

a 0 ∑ k = 1 m x k + a 1 ∑ k = 1 m x k 2 = ∑ k = 1 m x k y k

Onde teremos:

a 0 = ∑ k = 1 m x k 2 ∑ k = 1 m y k - ∑ k = 1 m x k y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

a 1 = m ∑ k = 1 m x k y k - ∑ k = 1 m y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

E quando temos a parábolas, teremos:

a 0 m + a 1 ∑ k = 1 m x k + a 2 ∑ k = 1 m x k 2

Para cada um desses sistemas, precisamos calcular uma batelada de termos e comparar os resultados.

Passo 2

Para calcular e equação linear, precisaremos calcular alguns termos como: x k ,   y k ,   x k 2 e x k y k e o somatório de cada um dos termos:

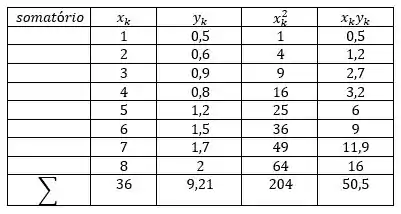
Aplicando na fórmula, teremos:

a 0 = ∑ k = 1 m x k 2 ∑ k = 1 m y k - ∑ k = 1 m x k y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

a 0 = 204 9,2 - ( 50,5 ) ( 36 ) 8 204 - 36 2 = 0,17284

E também:

a 1 = m ∑ k = 1 m x k y k - ∑ k = 1 m y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

a 1 = 10 50,5 - 36.9,2 10 204 - 36 2 = 0,2335

Aplicando na fórmula, teremos:

φ x k = a 0 + a 1 x k

φ x k = 0,2336 x + 0,173

Passo 3

Para calcular e equação da parábola, precisaremos calcular alguns termos como: x k ,   y k ,   x k 2 , x k 3 ,   x k 4 e x k y k ,   x k 2 y e o somatório de cada um dos termos:

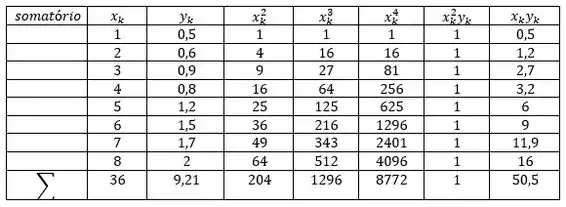
Montando um sistema com as informações dadas:

8 a 0 + 36 a 1 + 204 a 2 = 9,2

36 a 0 + 204 a 1 + 1296 a 2 = 50,5

2014 a 0 + 1296 a 1 + 8772 a 2 = 319,2

Solucionando o programa, teremos:

a 0 = 0,407

a 1 = 0,0774

a 2 = 0,0155

A solução final será dada:

p x = a 2 x 2 + a 1 x + a 0

y = 0,0155 a x 2 + 0,0774 x + 0,407

Passo 4

Vamos ver como ficam essas curvas e os pontos num gráfico?? O gráfico é esse:

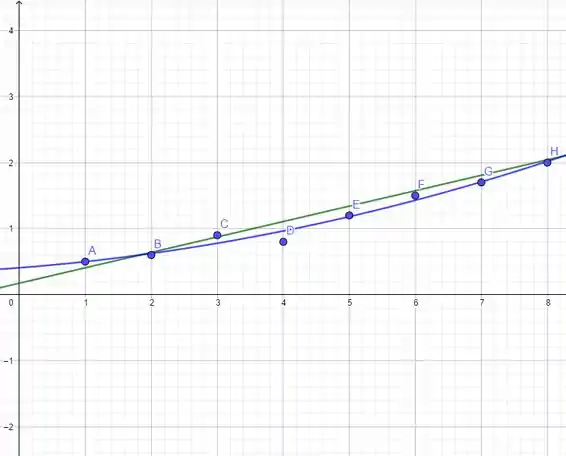
Então, se você reparar os pontos com as curvas, verá que a curva como parábola se ajusta melhor que a reta, já que ela passa por mais pontos no gráfico. Certo??

Só isso 😊

Resposta

Reta:

φ x k = 0,2336 x + 0,173

Parábola:

y = 0,0155 a x 2 + 0,0774 x + 0,407

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deseja-se aproximar uma função f definida em um intervalo [ a , b ] por uma função g x = x 2 ln ⁡ x 3 a + b x 2 usando o método dos mínimos quadrados.a) Qual é a função a ser minimizada?b) Qual é o si
Ajustar os valores da tabela:através de uma das famílias de funções: a e b x ,1 a + b x ,x a + b x Use o teste de alinhamento para decidir qual das funções melhor resolve o problema.O método dos mínim
Determinar a melhor solução para o sistema:
E possível aproximar diretamente uma função f ( x ) tabelada, por uma função do tipo: g x = a 1 + b cos ⁡ x usando o método dos mínimos quadrados? Se não for possível, qual é a transformação que deve
Resolver, pelo método dos mínimos quadrados, o sistema: