Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 3

Dada a tabela abaixo, faça o gráfico de dispersão dos dados e ajuste uma curva da melhor maneira possível:

Passo 1

Fala galerinha, tudo certinho?

Bom, esse exercício é para aplicarmos a ferramenta do método dos mínimos quadrados.

Olhando o gráfico de dispersão da função:

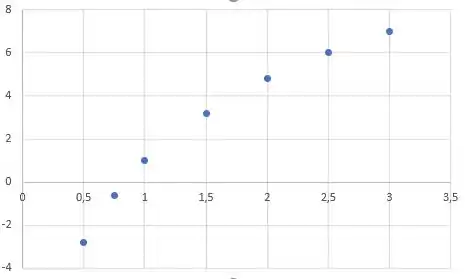
Perceba que o comportamento do gráfico se comporta como log ⁡   e podemos usar uma regra de ajuste de curvas para log ⁡   , onde:

Y = a ln ⁡ ( b x )

Onde:

Y = a ln ⁡ b + a ln ⁡ x

Onde :

a 0 = a ln ⁡ b

a 1 = a

y = ln ⁡ y

E a solução final vai ter a forma:

Y = a 0 + a 1 x

Passo 2

Para calcular e equação linear, precisaremos calcular alguns termos como: x k ,   y k ,   x k 2 e x k y k e o somatório de cada um dos termos.

Uma coisa que iremos fazer aqui para facilitar os nossos cálculos é fazer essa regressão na calculadora. Onde você aperta MODE+REG+LOG. Aí você vai inserir os dados você aperta SHIFT+1 onde a calculadora te dá o somatório de: x 2 ,   x ,   y , x y .

Caso você queira calcular manualmente é pegar cada valor de x e elevar ao quadrado, e cada y multiplicar por ln ⁡   . E o valor de x y = x . ln ⁡ y . Os valores dados são:

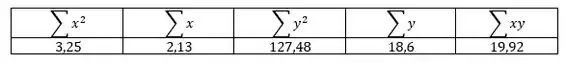
Agora, aperte SHIFT+2 na calculadora e passe até chegar em A e B, onde você terá a seguinte equação:

y = 5,48 ln ⁡ x + 0,989

Resposta

y = 5,48 ln ⁡ x + 0,989

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9. a) Considere:Através do teste de alinhamento, escolha uma das famílias de funções abaixo que melhor ajuste estes dados: a e b x , 1 / ( a + b x ) , x / ( a + b x ) b) Ajuste os dados do item acima
10. Aproxime a tabela abaixo por uma função do tipo g x = 1 + a e b x usando mínimos quadrados. Discuta seus resultados.
11. Considere a tabela...Por qual das funções x t = t a t + b ou y t = a b t você aproximaria a função u ( t ) ? Justifique sua resposta.
Considere a função: y t = - 1 , - π ≤ t ≤ 0 1 , 0 ≤ t ≤ π Verificar que a aproximação trigonométrica de grau 2: y t = a 0 + a 1 cos ⁡ t + b 1 sin ⁡ t + a 2 cos ⁡ 2 t + b 2 sin ⁡ 2 t Para y ( t ) é dad
Mostre que o conjunto das funções: { 1 , cos ⁡ t , sin ⁡ t , cos ⁡ 2 t , sin ⁡ 2 t ,… , sin ⁡ m t } e um sistema ortogonal em [ - π , π ]