Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 5.Exercícios - Ex. 8

Com que grau de precisão podemos calcular 115 usando interpolação sobre os pontos: x 0 = 100 , x 1 = 121 e x 2 = 144 ?

Passo 1

Faaaaaaaala meu caro, tudo certinho?

O que temos aqui é uam função x onde nesse caso x = 115 . O exercício nos fornece 3 valores diferentes de x ( 100 ,   121 ,   144 ) . Então temos uma coluna x e f ( x ) , onde podemos montar a tabela:

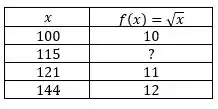
E é com esse conjunto de pontos que vamos montar o polinômio de grau 2 (já que temos 3 nós, n + 1 ) :

p 2 x = α 0 + α 1 x + α 2 x 2

Então, bora lá resolver!

Passo 2

Podemos encontrar o valor de f ( x ) de várias maneiras possíveis. Podemos montar o polinômio interpolador aplicando na fórmula de p 2 aplicando nos pontos dados:

p 2 100 = α 0 + α 1 100 + α 2 100 2 = 10

p 2 1 21 = α 0 + α 1 1 21 + α 2 1 21 2 = 11

p 2 1 44 = α 0 + α 1 1 44 + α 2 1 44 2 = 1 2

Com isso conseguimos montar um sistema matricial:

1 100 100 2 1 121 121 2 1 144 144 2 α 0 α 1 α 2 = 10 11 12

Onde resolveremos esse sistema e encontraremos o resultado.

Maaaaaaaas, existe uma forma mais simples de resolver essa parada!

Passo 3

Vamos interpolar do modo mais simples, usando a calculadora científica. Aperte o botão MODE+REG3+LIN1.

Agora você vai inserir os conjuntos de pontos da tabela:

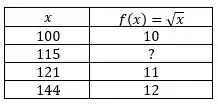
O modo de inserir os pontos na calculadora é ( v a l o r   d e   x ,   v a l o r   d e   y ) e M + , inserir todos os valores até chegar em n=3.

A calculadora vai juntar os pontos, você aperta s h i f t + 2   e aperte a seta até chegar em A e B, onde construímos a equação:

p 2 x = 5,4735 + 0,04542 x

Qual o valor para x = 115 :

p 2 115 = 5,4735 + 115.0,04542 = 10,6868

Passo 4

O valor real de 115 = 10,7238 , o erro será a diferença absoluta que será dada por:

E R % = V a l o r   r e a l - V a l o r   e s t i m a d o V a l o r   r e a l = 10,7238 - 10,6868 10,7238 * 100

E R = 0,25 %

Isso significa que nosa precisão será 100 - E R = 99,75 %

Resposta

Valor estimado 10,6868 e Precisão 99,75 %  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de números primos menores que x é denotado por π ( x ) e vale a tabela:a) Determinar pelo método dos mínimos quadrados, para os dados acima, expressão do tipo: π x = a + b x log 10 ⁡ x b) Est
A tabela a seguir lista o número de acidentes em veículos motorizados no Brasil em alguns anos entre 1980 e 1998.a) Calcule a regressão linear do número de acidentes no tempo. Use-a para prever o núme
(Ajuste na curva tração/deformação de um tipo de aço). Feito um ensaio de tração em uma barra de um tipo de aço, em uma máquina universal de Amsler, foram obtidos os valores constantes da tabela a seg
Em uma floresta densa, dois formigueiros inimigos, separados por um rio, travam uma longa batalha. Um dos formigueiros, visando acabar gradativamente com a espécie inimiga, dá uma cartada fatal, seque
Os dados das tabelas a seguir mostram a quantidade de alcatrão e nicotina (em miligramas) para várias marcas de cigarro com e sem filtro i ) Calcule as regressões lineares do tipo a x + b para a relaç