Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 31.f
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Passo 1
Eai pessoal, para saber sobre a solução de um sistema linear, a gente tem que primeiro verificar o número de variáveis e o número de equações do sistema!
Passo 2
Nesse caso, temos apenas a equação:
Como essa matriz tá bem bonitinha, vamos começar já escalonando ela!
Passo 3
Primeiro temos:
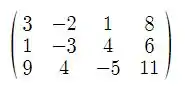
Agora vamos trocar :
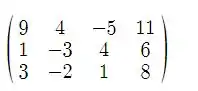
Trocando por :
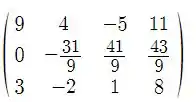
Agora vamos trocar por :
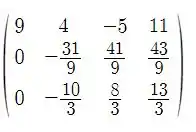
Agora vamos trocar por :
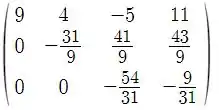
E pronto, isso daqui tá escalonado!
Daqui a gente pode ver que esse sistema tem uma solução única!
Resposta
solução única.
Exercícios de Livros Relacionados
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.