Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 3.Exercícios - Ex. 31.b
Para cada um dos sistemas lineares a seguir, analise a existência ou não de solução, bem como unicidade de solução, no caso de haver existência.
Passo 1
Eai pessoal, para saber sobre a solução de um sistema linear, a gente tem que primeiro verificar o número de variáveis e o número de equações do sistema!
Passo 2
Nesse caso, temos apenas a equação:
Nesse caso, temos a mesma quantidade de equações e incógnitas, temos que passar para o próximo teste, que é calcular o determinante da matriz , sendo o sistema representado por .
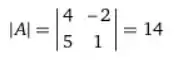
Agora sabemos que o sistema pode não ter soluções ou pode ser determinado e de solução única!
Passo 3
Agora, vamos ter que escalonar a seguinte matriz:
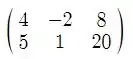
Trocando as fileiras, teremos:
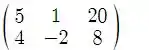
Agora trocando por
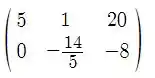
Daqui podemos ver que o sistema tem solução única!
Resposta
Solução única.