A curvatura de uma coluna delgada sujeita a uma carga pode ser modelada por:

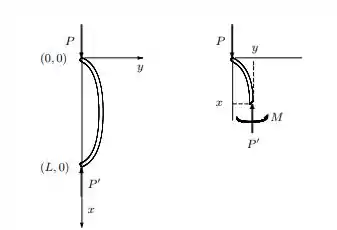
Onde especifica a curvatura, é o momento de curvatura, E é o modulo de elasticidade, e é o momento de inércia da seção transversal sobre o eixo neutro. Considerando o corpo livre na Figura é claro que o momento de curvatura em . Substituindo esse valor na equação

, onde

Isto pode ser entendido como uma deformação da carga porque elas representam os níveis nos quais as colunas movimentam-se em cada deformação sucessiva. Na prática, em geral, o autovalor correspondente à é o de interesse porque a quebra usualmente ocorre quando a primeira coluna se deforma. Assim, a carga crítica pode ser definida como:

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide uma curvatura de uma coluna delgada sujeita a uma carga pode ser modelada por:

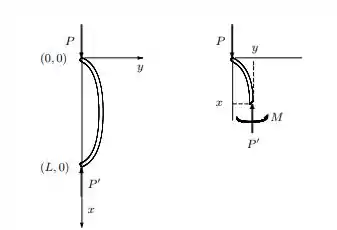
Onde especifica a curvatura, é o momento de curvatura, E é o modulo de elasticidade, e é o momento de inércia da seção transversal sobre o eixo neutro. Considerando o corpo livre na Figura é claro que o momento de curvatura em . Substituindo esse valor na equação

, onde

Isto pode ser entendido como uma deformação da carga porque elas representam os níveis nos quais as colunas movimentam-se em cada deformação sucessiva. Na prática, em geral, o autovalor correspondente à é o de interesse porque a quebra usualmente ocorre quando a primeira coluna se deforma. Assim, a carga crítica pode ser definida como:

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.