Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 7.Problemas Aplicados e Projetos - Ex. 5
No problema , para três nós interiores você obteve o seguinte sistema:
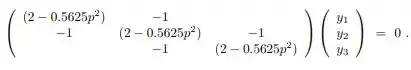
a) Mostre que dividindo cada equação por , obtêm-se:
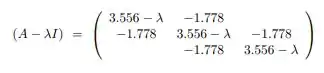
onde , e que a expansão do determinante fornece:
b) Mostre que o mesmo polinômio pode ser obtido aplicando-se o método de Leverrier-Faddeev à matriz:
c) Usando o polinômio característico obtido em b), determine os autovalores de B, usando método numérico `a sua escolha.
d) Usando o método de Jacobi, determine os autovalores e autovetores da matriz B
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide dado o problema para três nós interiores você obteve o seguinte sistema:
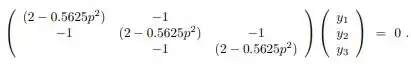
a) Mostre que dividindo cada equação por , obtêm-se:
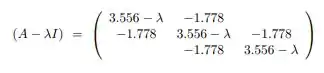
onde , e que a expansão do determinante fornece:
b) Mostre que o mesmo polinômio pode ser obtido aplicando-se o método de Leverrier-Faddeev à matriz:
c) Usando o polinômio característico obtido em b), determine os autovalores de B, usando método numérico `a sua escolha,
d) Usando o método de Jacobi, determine os autovalores.
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha sabendo que para três nos interiores temos o sistema,
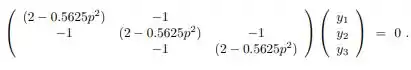
Temos que na letra (a) para determinar a expansão dado,
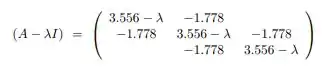
Temos,
Já na letra (b) para mostrar que o polinômio pode ser obtido por Leverrier, temos
Ficando,
Logo temos,
Ficando,
Passo 3
Já na letra tendo o polinômio característico, temos
Temos,
Ficando,
E por fim na letra (d) temos que por meio de Jacobi dado,
Com isso temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b)
c)
d)