No problema 7.3 foi razoavelmente fácil obter os autovalores pois era conhecida a expressão analítica da solução, o que em geral não acontece na prática. Assim, podemos obter os autovalores de (7.19), substituindo a derivada segunda pela diferença dividida central, isto é, substituindo por:
Fazendo isso, podemos escrever (7.20) como:
Escrevendo esta equação para uma série de nós ao longo do eixo da coluna, obtém-se um sistema de equações homogêneas. Por exemplo, se a coluna é dividida em cinco segmentos (isto é, quatro nós interiores), o resultado é:
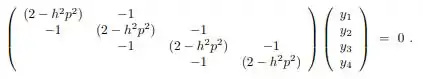
Considerando os mesmos dados do problema 7.3 determine os autovalores para os casos:
a) um;
b) dois;
c) três;
d) quatro nós interiores, usando método numérico à sua escolha. Lembre-se: desde que , segue que para um nó interior , para dois nós interiores , etc.
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide no problema 7.3 foi razoavelmente fácil obter os autovalores pois era conhecida a expressão analítica da solução, o que em geral não acontece na prática. Assim, podemos obter os autovalores de (7.19), substituindo a derivada segunda pela diferença dividida central, isto é, substituindo por:
Fazendo isso, podemos escrever (7.20) como:
Escrevendo esta equação para uma série de nós ao longo do eixo da coluna, obtém-se um sistema de equações homogêneas. Por exemplo, se a coluna é dividida em cinco segmentos (isto é, quatro nós interiores), o resultado é:
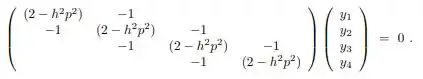
Considerando os mesmos dados do problema 7.3 determine os autovalores para os casos:
a) um;
b) dois;
c) três;
d) quatro nós interiores, usando método numérico à sua escolha. Lembre-se: desde que , segue que para um nó interior , para dois nós interiores , etc.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galerinha dado a equação homogênea:
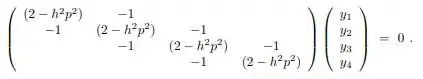
Temos que na letra (a) para determinarmos os autovalores para o caso 1 temos,
Já na letra (b) para dois termos,
E na letra para três termos,
E por fim na letra (d) pra nós temos,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.

Resposta
a)
b)
c)
d)