Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 37

A equação 𝑥 3 − 2 𝑥 − 1   = 0 possui apenas uma raiz positiva.

a) De acordo com o princípio da bissecção, esta raiz positiva deve estar em qual dos intervalos: (0,1), (1,2), (2,3)? Por que?

b) Se desejássemos também pesquisar as raízes negativas usando intervalos de amplitude 1 2 , até o ponto − 2   , em que intervalos seriam encontradas tais raízes?

c)Obtenha a menor raiz negativa (em módulo), usando o método das Secantes. Trabalhe com arredondamento para 3 casas decimais.

Passo 1

Oláaaa, vamos para mais um exercício. Começando pelo item a teremos que lembrar daquele princípio do método da bissecção, em que, existe raiz em um dado intervalo 𝑎 ,   𝑏 se 𝑓 𝑎 × 𝑓 𝑏 < 0 , ou seja, o valor numérico da função para 𝑎   ou 𝑏   deve ser negativo enquanto o outro, positivo, dessa forma temos a garantia que o gráfico da função corta o eixo x em algum ponto.

Vamos fazer o teste para os intervalos disponibilizados pelo enunciado:

Intervalo 0 ,   1 :

𝑓 0 = 0 3 − 2 0 − 1   =   − 1

𝑓 1 = 1 3 − 2 1 − 1   =   − 2

Ambos são negativos, logo não tem raiz nesse intervalo.

Intervalo 1 ,   2 :

𝑓 1   =   − 1

𝑓 2   =   2 3 − 2 2 − 1 =   3

Obtemos um valor negativo e um positivo, logo temos raiz no intervalo e já explicamos o motivo. Vamos analisar o último intervalo:

Intervalo 2 ,   3 :

𝑓 2 =   3

𝑓 3 =   3 3 − 2 3 − 1 =   20

Dois valores positivos, logo não temos raiz.

Passo 2

Partindo para o item b devemos, inicialmente, analisar o gráfico da função para olharmos em quais intervalos ela corta o eixo x em sua parte negativa:

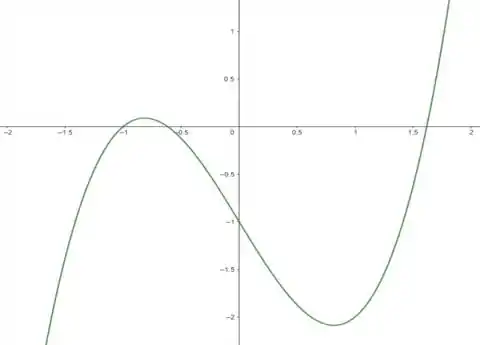
Como você pode ver, se seguirmos em intervalos de 1 2 , teremos raiz entre − 1 , − 0.5   𝑒   − 2 ,   − 1 , de acordo com o princípio da bissecção que já comentamos.

Passo 3

Por fim no item c iremos aplicar o método das secantes para encontrar a menor raiz negativa que já sabemos que está entre − 1 ,   0.5 , porém, umas das raízes é -1, logo iremos usar um intervalo mais estreito, − 0.6 ,   0.5 , então eles serão nossos valores iniciais. Aplicando o método considerando 𝑥 0 = − 0.6   𝑒   𝑥 1 = − 0.5   :

𝑥 𝑘 + 1 = 𝑥 𝑘 − 1 𝑓 𝑥 𝑘 − 𝑥 𝑘 𝑓 𝑥 𝑘 − 1 𝑓 𝑥 𝑘 − 𝑓 𝑥 𝑘 − 1

𝑥 2 = − 0.6 𝑓 − 0.5 + 0.5 𝑓 − 0.6 𝑓 − 0.5 − 𝑓 − 0.6 ≈ − 0.6147

Continuando as iterações obtemos:

𝑥 3   ≈ − 0.6174  

𝑥 4   ≈ − 0.6180  

Ufa finalizamos o exercício, até o próximo!!!

Resposta

a) Intervalo 1 ,   2 .

b) raiz em − 1   e entre − 1 ,   − 0.5 .

c) 𝑥 _ ≈ − 0.6180   .

Exercícios de Livros Relacionados

Considere a equação: 𝑓 𝑥   =   2 𝑥 2 − 5 𝑥 + 2 = 0     , cujas raízes são. Considere ainda os processos iterativos:a) 𝑥 𝑘 + 1 =   2 𝑥 2 + 2 5 ,   b) 𝑥 𝑘 + 1 =   5 𝑥 𝑘 2 − 1 .   Qual dos doi
A equação: x 2 - a   =   0     possui uma raiz x ¯   =   a     . Explicar algebricamente e geometricamente por que a sequência x k , obtida através do processo iterativo definido por: x k + 1 = a x k
Mostre que 𝑥 3 − 2 𝑥 − 17 = 0 tem apenas uma raiz real e determine seu valor correto em até 2 casas decimais usando o método de Newton.
Mostre que as seguintes equações possuem exatamente uma raiz e que em cada caso a raiz está no intervalo 0.5 ,   1   .a) 𝑥 2 + l n l n𝑥= 0 Determine essas raízes, com duas casas decimais corretas, u
Mostre que as seguintes equações possuem exatamente uma raiz e que em cada caso a raiz está no intervalo 0.5 ,   1   .b) 𝑥 𝑒 𝑥 − 1 = 0 Determine essas raízes, com duas casas decimais corretas, usan