Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 31b

Aplique o método da bissecção para resolver:

b)

Obtendo em cada caso a e b (iniciais) graficamente.

Passo 1

Opa, tudo beleza? Semelhantemente ao item a iremos usar o método da bissecção para achar uma raiz aproximada da função. Primeiramente vamos descobrir graficamente onde a raiz está localizada:

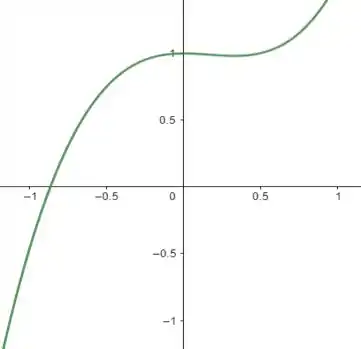
Pelo gráfico podemos ver que a raiz está entre –1 e –0.5 .

Passo 2

Aplicando o método da bissecção no intervalo :

Como você já tá craque no passo a passo, vou passar direto os intervalos que obtemos ao aplicar o método ok? Mas lembre-se de analisar o valor numérico de cada novo intervalo com o intervalo inicial para realizar as substituições, para isso considere:

Com isso, os intervalos que você deve obter tem que ser próximos a:

Se você chegou em algo próximo comemora, porque acabou! Até mais.

Resposta

Exercícios de Livros Relacionados

Pelo Teorema do Valor Médio temos que x k + 1 - ξ = φ ' ( c k ) ( x k - ξ ) com c k entre x k e ξ . Analise os sinais de x j - ξ , j = 0,1 , . . .

O método da bissecção pode ser aplicado sempre que f ( a ) f ( b )0 , mesmo que f ( x ) tenha mais que um zero em ( a ,b ) . Nos casos em que isto ocorre, verifique, com o auxílio de gráficos, se é po

Se no método da bissecção tomarmos sistematicamente x = a k + b k 2 , teremos que | x _ - ξ | ≤ b k - a k 2 .Considerando este fato:estime o número de iterações que o método efetuará;escreva um novo a

Usando a regra de sinal de descartes, verifique que a equação p x = 3 x 5 - x 4 - x 3 + x + 1 = 0 pode ter duas raízes reais no intervalo.

O problema: resolva 𝑓 𝑥 = 𝑥 + l n l n𝑥= 0 pode ser transformado num problema equivalente da forma 𝑥 = Ψ 𝑥 . Para o processo iterativo definido por 𝑥 𝑘 + 1 = Ψ 𝑥 ; Analisar a c