Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios - Ex. 7

A equação: x 2 - a   =   0 possui uma raiz x ¯   =   a . Explicar algebricamente e geometricamente por que a sequência x k , obtida através do processo iterativo definido por: x k + 1 = a x k , não converge para a qualquer que seja o valor de x 0   .

Passo 1

Eaii? Tudo em cima? Vamos novamente utilizar as regras de convergência de processos iterativos lineares para resolver esta questão, em específico, utilizaremos a seguinte expressão:

ψ x <   1

Que, dadas ψ x   e   ψ ' x contínuas em R   , teremos a certeza de que a expressão iterativa convergirá para a raiz x ¯ . Dessa forma poderemos expressar algebricamente o que o exercício pede.

Passo 2

Utilizando a expressão citada acima na derivada da função:

ψ ' x =   2 x   < 1   →   - 1 2 <   x   <   1 2

Logo a deve estar entre o intervalo que acabamos de encontrar.

Passo 3

Analisando geometricamente a função, considerando a=1, obtemos:

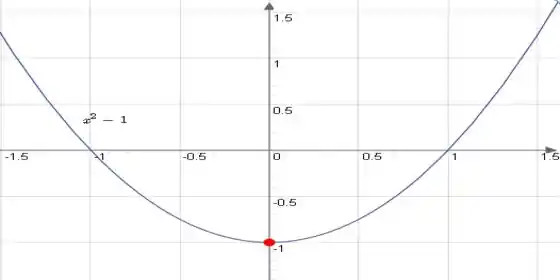
Analisando o gráfico e impondo que ψ ' x   <   1 , vemos que em qualquer vizinhança de a existe pelo menos um ponto onde ψ ' x = 1 , o que nos prova que independentemente do valor de x 0   , x k + 1 = a x k não converge para a .

Resposta

Na vizinhança de a existem pontos onde ψ ' x   =   1 .

Exercícios de Livros Relacionados

Mostre que 𝑥 3 − 2 𝑥 − 17 = 0 tem apenas uma raiz real e determine seu valor correto em até 2 casas decimais usando o método de Newton.
Mostre que as seguintes equações possuem exatamente uma raiz e que em cada caso a raiz está no intervalo 0.5 ,   1   .a) 𝑥 2 + l n l n𝑥= 0 Determine essas raízes, com duas casas decimais corretas, u
Mostre que as seguintes equações possuem exatamente uma raiz e que em cada caso a raiz está no intervalo 0.5 ,   1   .b) 𝑥 𝑒 𝑥 − 1 = 0 Determine essas raízes, com duas casas decimais corretas, usan
A equação 𝑥 3 − 2 𝑥 − 1   = 0   possui apenas uma raiz positiva.a) De acordo com o princípio da bissecção, esta raiz positiva deve estar em qual dos intervalos: (0,1), (1,2), (2,3)? Por que?b) Se de
A equação 𝑓 𝑥 = 𝑒 𝑥 − 3 𝑥 2 = 0 tem três raízes. Um método iterativo pode ser definido usando a preparação óbvia da equação: 𝑥 = ± 𝑒 𝑥 3 i) Verificar que começando com x0 = 0 haverá convergênc