Considere o movimento horizontal do conjunto massa mola mostrado na figura,

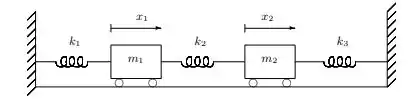
As deflexões horizontais são medidas relativamente à posição de equilíbrio estático. As molas possuem rigidez , que são as forças requeridas para estender ou comprimir cada mola de uma unidade de comprimento. As equações de movimento são:

a) Se é o vetor deflexão então podemos reescrever as equações acima na forma:

b) Mostre que a substituição:

onde é um vetor do , com , leva ao problema de autovalores: onde . Os possíveis valores que pode assumir são as frequências naturais de vibração do sistema.

c) Se determine os autovalores e autovetores de , por método numérico à sua escolha.

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide considerando o movimento horizontal do conjunto massa mola mostrado na figura,

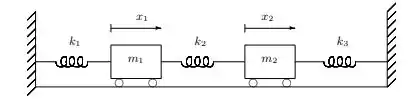
As deflexões horizontais são medidas relativamente à posição de equilíbrio estático. As molas possuem rigidez , que são as forças requeridas para estender ou comprimir cada mola de uma unidade de comprimento. As equações de movimento são:

a) Se é o vetor deflexão então podemos reescrever as equações acima na forma:

b) Mostre que a substituição:

onde é um vetor do , com , leva ao problema de autovalores: onde . Os possíveis valores que pode assumir são as frequências naturais de vibração do sistema.

c) Se determine os autovalores e autovetores de , por método numérico à sua escolha.

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.