Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 8.Problemas Aplicados e Projetos - Ex. 18
Uma refinaria pode comprar dois tipos de petróleo bruto: leve ou pesado. Os custos por barril desses tipos são respectivamente (unidade adotada: reais). As seguintes quantidades de gasolina , querosene e combustível de avião são produzidas a partir de um barril de cada tipo de petróleo:
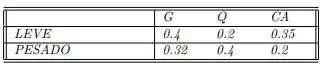
Note que do petróleo bruto, leve e pesado, são perdidos respectivamente durante o processo de refinamento. A refinaria deve entregar barris de Gasolina, barris de Querosene e barris de Combustível para aviões, sendo que há disponibilidade de mil reais para a compra de petróleo bruto leve e pesado. O objetivo é determinar tais quantidades. Assim, denotando por a quantidade de petróleo bruto leve e por a quantidade de petróleo bruto pesado, em barris chegamos ao sistema:
que é um sistema incompatível.
a) Usando o método dos mínimos quadrados determine .
b) Pode-se obter como quantidades não inteiras?
c) Calcule o resíduo, isto é:
onde são os elementos da matriz do sistema e é o vetor independente.
d) Quais as quantidades de gasolina, querosene e combustível para aviões produzidas?
Passo 1
Falaaaaa rapaziada tudo blz?
Nessa questão do livro de cálculo numérico de Franco e Neide Uma refinaria pode comprar dois tipos de petróleo bruto: leve ou pesado. Os custos por barril desses tipos são respectivamente (unidade adotada: reais). As seguintes quantidades de gasolina , querosene e combustível de avião são produzidas a partir de um barril de cada tipo de petróleo:
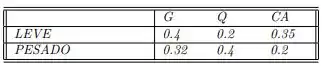
Note que do petróleo bruto, leve e pesado, são perdidos respectivamente durante o processo de refinamento. A refinaria deve entregar barris de Gasolina, barris de Querosene e barris de Combustível para aviões, sendo que há disponibilidade de mil reais para a compra de petróleo bruto leve e pesado. O objetivo é determinar tais quantidades. Assim, denotando por a quantidade de petróleo bruto leve e por a quantidade de petróleo bruto pesado, em barris chegamos ao sistema:
que é um sistema incompatível.
a) Usando o método dos mínimos quadrados determine .
b) Pode-se obter como quantidades não inteiras?
c) Calcule o resíduo, isto é:
onde são os elementos da matriz do sistema e é o vetor independente.
d) Quais as quantidades de gasolina, querosene e combustível para aviões produzidas?
Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.
Passo 2
Então galera na letra (a) para determinarmos o método dos mínimos quadrados no sistema,
Temos,
Ficando,
Já na letra (b) podemos dizer que sim podem ter resultados não inteiros como o de foi encontrado
Já na letra para calcular,
Temos,
E por fim na letra (d) temos que a quantidade de combustível pode ser definida por,
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
a)
b) sim podem ter resultados não inteiros como o de foi encontrado
c)
d)