Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Problemas Aplicados e Projetos - Ex. 12
Um tanque de vaporização flash é alimentado com por uma corrente de gás natural componentes, como mostrado na
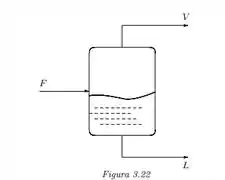
As correntes de líquido e vapor são designadas por e , respectivamente. As frações molares dos componentes na alimentação, nas correntes de vapor e líquido são designadas por , respectivamente. Assumindo equilíbrio líquido-vapor em estado estacionário, segue que:
Onde é o balanço global, é o balanço individual, é a relação de equilíbrio e, é a constante de equilíbrio para o i-ésima componente na pressão e temperatura do tanque:
Das equações acima e do fato de
Mostra-se:
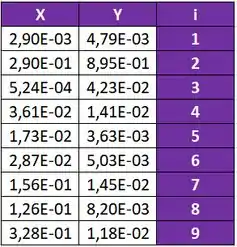
Supondo que , calcule o valor de , com duas casas decimais corretas, resolvendo a equação , para a corrente de gás natural, à temperatura de e pressão de , para cada um dos componentes da tabela a seguir:
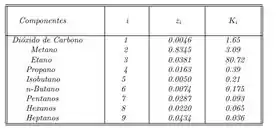
Para cada valor de , calcule os valores de , de e de .
Passo 1
Opa galerinha do Responde Aí, meu nome é jacyara e hoje vamos resolver uma questãozinha de cálculo numérico.
A questão te informa qual é a função objetivo do problema que é essa aqui:
E te dá os dados necessários para resolver o probleminha que é dado através dessa tabelinha aqui:
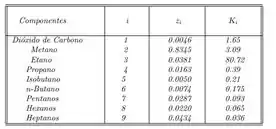
E pede para calcular os valores de e para uma vazão de alimentação de .
O cálculo de e não é problema, porém, o cálculo de é um problema pois não conseguimos isolar a variável da função objetivo, sendo assim, temos aqui uma equação não linear e para resolvê-la vamos utilizar o método de Newton por ser um método que tem uma convergência mais acelerada.
E como o resultado que uma aproximação com 2 casas decimais corretas, vamos utilizar uma aproximação de para garantir isso.
Bem, mas o que é o método de Newton né?
Eu detesto decorar, mas sugiro que em cálculo numérico decore os passos dos métodos porque é uma ajuda imensa na resolução das questões. Enfim, o método de newton de equações não lineares é o seguinte:
- Primeiro passo: estimativa inicial.
- Segundo passo: Calcular o valor do sistema com a estimativa inicial.
- Terceiro passo: verificar a convergência.
- Quarto passo: Método de Newton – cálculo da derivada
- Quinto passo: Calcular o incremento e a estimativa atualizada.
- Sexto passo: Repetir os passos anteriores até atingir a convergência.
Como a questão não definiu o critério de convergência, vamos definir um valor de por ser um valor pequeno e se aproximar do 0 e já é um valor de bom tamanho, valores menores do que esse podem gerar passos demasiados.
Agora que temos o roteiro, vamos na prática ver como isso funciona. E aí? Podemos ir? Vamos lá.
Passo 2
Primeiramente, precisamos da derivada para realizar o calculo do método de Newton e, portanto, temos:
Portanto, temos:
Como temos 9 componentes, vamos expandir essa soma até e temos as seguintes equações:
Como as equações aqui são grandes, recomendo utilizar alguma ferramenta de calculo para otimizar o processo.
Ahh nossa estimativa inicial né? Bem, olha os dados do gás natural. Só existe componentes extremamente voláteis então imaginamos que quase tudo aí deve ser gás e vamos utilizar uma estimativa inicial de belezinha?
Agora vamos aplicar o método de Newton.
Passo 3
Aplicando o método de newton, temos:
- Primeiro passo:
- Segundo passo:
- Terceiro passo: verificar a convergência.
- portanto, temos que satisfaz a equação e é uma solução com uma aproximação de
Passo 4
Para calcular as demais variáveis temos que:
Portanto:
E partindo da segunda equação temos:
Sendo assim temos:
E analogamente temos:
Logo, para o cálculo das composições do liquido e do vapor temos que:
Substituindo os valores de e temos:
E calculando existente na seguinte tabela:
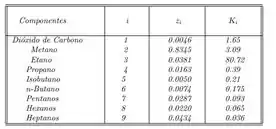
Temos que:
Grandinha né? Mas e aí, sacou? Responde Ai e vlwwwww.
Resposta
Todas as questões foram devidamente discutidas nos passos anteriores.