Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Problemas Aplicados e Projetos - Ex. 7
Quando um capacitor carregado é ligado com uma resistência , um processo de descarga do capacitor ocorre. Durante este processo, uma variável no tempo é estabelecida no circuito. Sua variação com o tempo se dá de forma decrescente e exponencial, de acordo com a expressão:
onde é a corrente, é a carga inicial do capacitor, sua capacitância, a resistência e o parâmetro tempo.
Definindo , o instante em que , corresponde àquele em que a corrente percorre o circuito.
Determinar nos seguintes casos:
- , , ,
- , , ,.
Passo 1
E aí galera do Responde Ai, quem fala aqui é a Jacyara e estamos aqui para resolver uma questãozinha de cálculo numérico.
A questão te fornece a questão de funcionamento de um capacitor que é a seguinte:
Aí a questão te pergunta o seguinte, quais os valores de na qual a igualdade abaixo é verdade
Nas seguintes condições:
- , , ,
- , , ,.
A questão não informa qual método deve ser utilizado para resolver, porém, a questão leva acreditar que se deve resolver por algum método numérico e vamos utilizar o método para resolver.
O método que vamos utilizar é o método de newton, pois, é um método cuja a convergência tende a ser mais acelerada, e o método é classificado pela seguinte sequência de passos:
- Primeiro passo: estimativa inicial.
- Segundo passo: Calcular o valor do sistema com a estimativa inicial.
- Terceiro passo: verificar a convergência.
- Quarto passo: Método de Newton – cálculo da derivada
- Quinto passo: Calcular o incremento e a estimativa atualizada.
- Sexto passo: Repetir os passos anteriores até atingir a convergência.
Como a questão não definiu o critério de convergência, vamos definir um valor de por ser um valor pequeno e se aproximar do 0 e já é um valor de bom tamanho, valores menores do que esse podem gerar passos demasiados.
Agora que temos o roteiro, vamos na prática ver como isso funciona. E aí? Podemos ir? Vamos lá.
Passo 2
Primeiramente, precisamos da equação não linear e essa equação nos é informada na nossa questãozinha.
Calculando a derivada para o método de newton temos:
E derivando a equação temos que:
Agora que temos as funções a derivada, precisamos aplicar o método de newton em cada equação e encontrar a raiz de cada equação.
Mas antes de tudo, vamos fazer uma estimativa né? Como encontrar essa estimativa?
Como cada alternativa é uma situação diferente, precisamos de uma estimativa para cada alternativa, então vamos responder nos próximos passos.
Agora vamos utilizar o método de newton, belezinha? Vamos lá
Passo 3
Para resolver a alternativa a) precisamos procurar a estimativa da função, portanto temos que utilizando os dados da letra a) que é dado por:
, , ,
Gerando o seguinte gráfico:
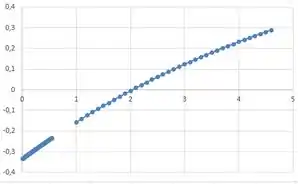
Portanto, temos que a melhor estimativa é em . Sendo assim, temos que a raiz da equação é encontrada através da seguinte equação:
E para resolver a questão vamos utilizar o método que foi apresentado no passo 1, vamos chutar uma estimativa inicial , portanto temos que:
- Primeiro passo:
- Segundo passo:
- Terceiro Passo: , portanto é raiz
Essa foi rapidinho né?
Passo 4
Agora precisamos resolver a mesma equação com a situação mencionada na alternativa b),
Cujo os dados é os seguintes:
, , ,.
Gerando a seguinte equação:
Utilizando a mesma estimativa da alternativa a), temos que:
- Primeiro passo:
- Segundo passo:
- Terceiro Passo: , portanto é raiz
Essa foi rapidinha né? Iae sacou? Responde ai e vlwwwwwwwwww