Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios - Ex. 18

Usando o método iterativo linear determinar a solução de:

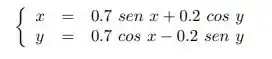
Próxima a 0.5,0.5 .

Passo 1

Eaí! Tudo bem?? Utilizar o método iterativo linear para resolver este sistema de equações não lineares. Para isso, devemos fazer algo semelhante ao método do ponto fixo que foi utilizado em questões anteriores, adotando:

Porém, o enunciado já nos forneceu as equações do sistema prontas para substituir os valores, ou seja, as transformações já foram feitas e é só partir para os cálculos.

Passo 2

Realizando as iterações:

𝑥 1 = 𝑓 𝑥 0 , 𝑦 0 = 0.7 𝑠 𝑒 𝑛 0.5 + 0.2 c o s c o s   0.5   = 0.511114

𝑦 1 = 𝑔 𝑥 0 , 𝑦 0 = 0.7 c o s c o s   0.5   − 0.2 𝑠 𝑒 𝑛 0.5 = 0.518423

Com isso, a solução aproximada do sistema foi encontrada!

Resposta

𝑥 1 = 0.511114  

𝑦 1 = 0.518423  

Exercícios de Livros Relacionados

Resolva o exercício 23 usando agora a sequência de Sturm.
Determinar, pelo método das secantes, uma raiz de cada uma das equações:b) l o g l o g𝑥− c o s c o s𝑥= 0
Determinar, pelo método das secantes, uma raiz de cada uma das equações:c) 𝑒 − 𝑥 − l o g l o g𝑥= 0
A equação f x = x 3 - 0.5 = 0 possui uma raiz entre 0.5 e 1.0 . usando o método de Regula Falsi e o algoritmo de Briot-Ruffini determinar essa raiz com precisão de 10 - 2 .