Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Máximos e Mínimos

Ver Todos os Exercícios

Teoria

Fala aí! Hoje vamos aprender um pouquinho mais sobre máximos e mínimos, tá preparado?

Então me acompanha até o final, que preparei um resuminho de tudo o que você precisa saber, junto de um vídeo com exercícios resolvidos passo a passo 🥰.

Veja também 🤩

O que são Pontos Máximos e Mínimos?

Um ponto de máximo é um ponto na função maior que os pontos próximos a ele.

Olha só pra esses exemplos aqui e tenta enxergar isso daí

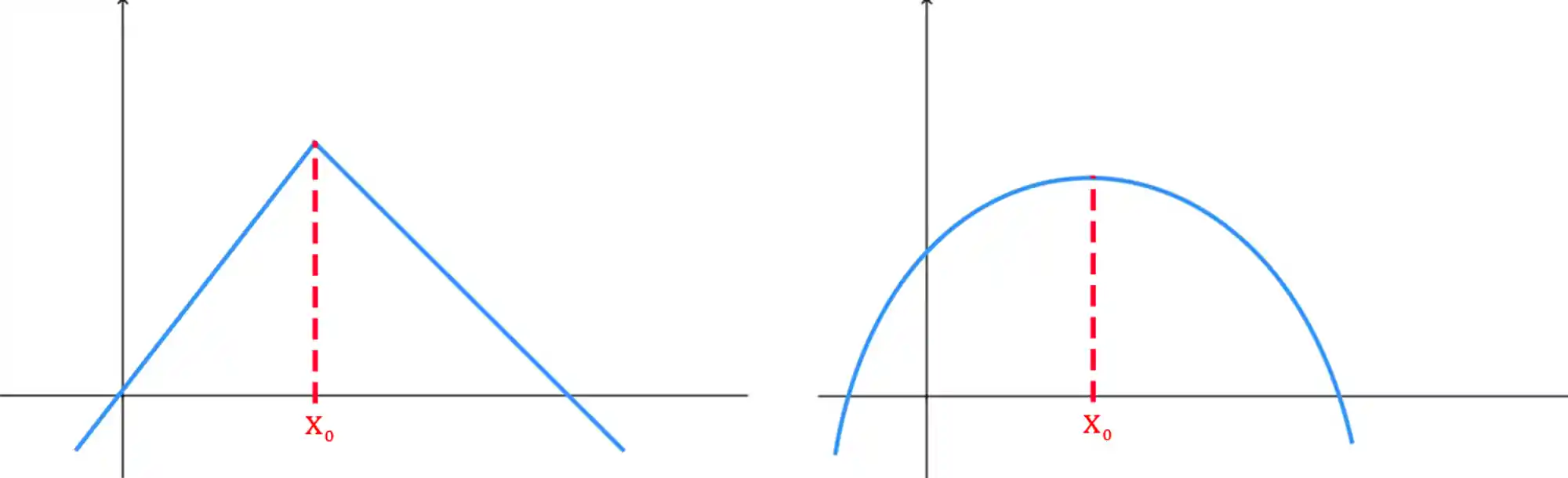
Gráfico com os pontos de máximo evidenciados.
Gráfico com os pontos de máximo evidenciados.

Conseguiu? Imagino que só batendo o olho você consegue ver que aquele ali é o ponto que vai assumir o maior valor de , por isso chamamos ele de ponto de máximo.

E o inverso vale para os pontos de mínimo: um ponto de mínimo é um ponto na função menor que os pontos próximos a ele.

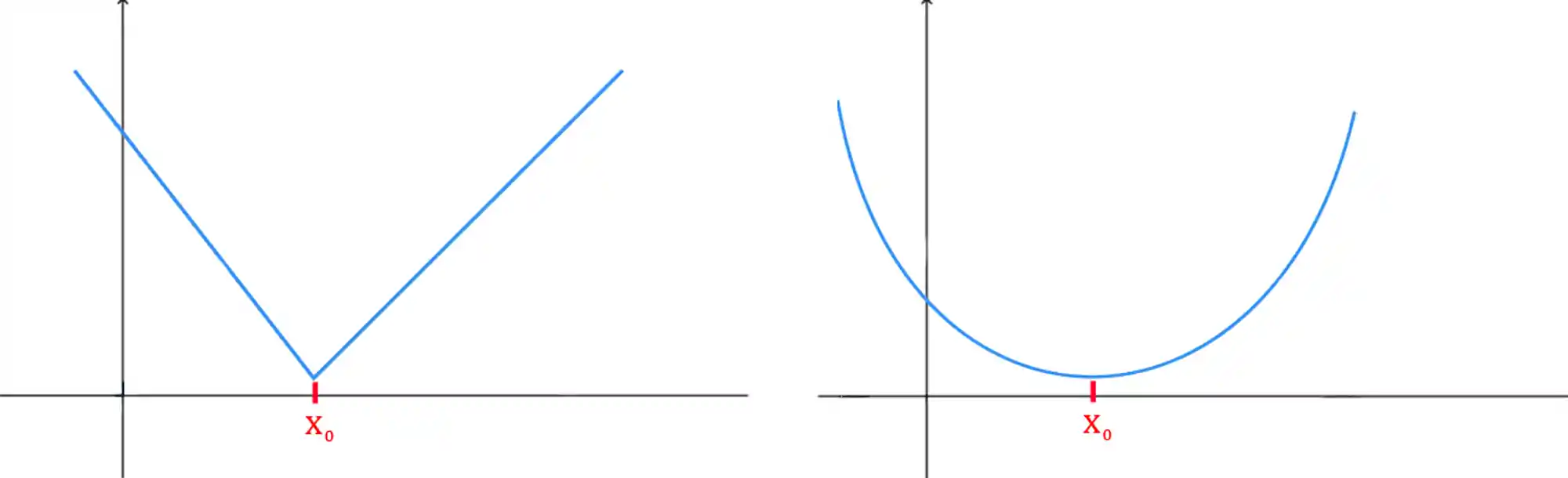
Gráfico com os pontos de mínimo evidenciados.
Gráfico com os pontos de mínimo evidenciados.

Máximos e Mínimos Absolutos ou Locais

Beleza, mas esses exemplos aí tão muito básicos, né? Bora pegar um mais complicadinho:

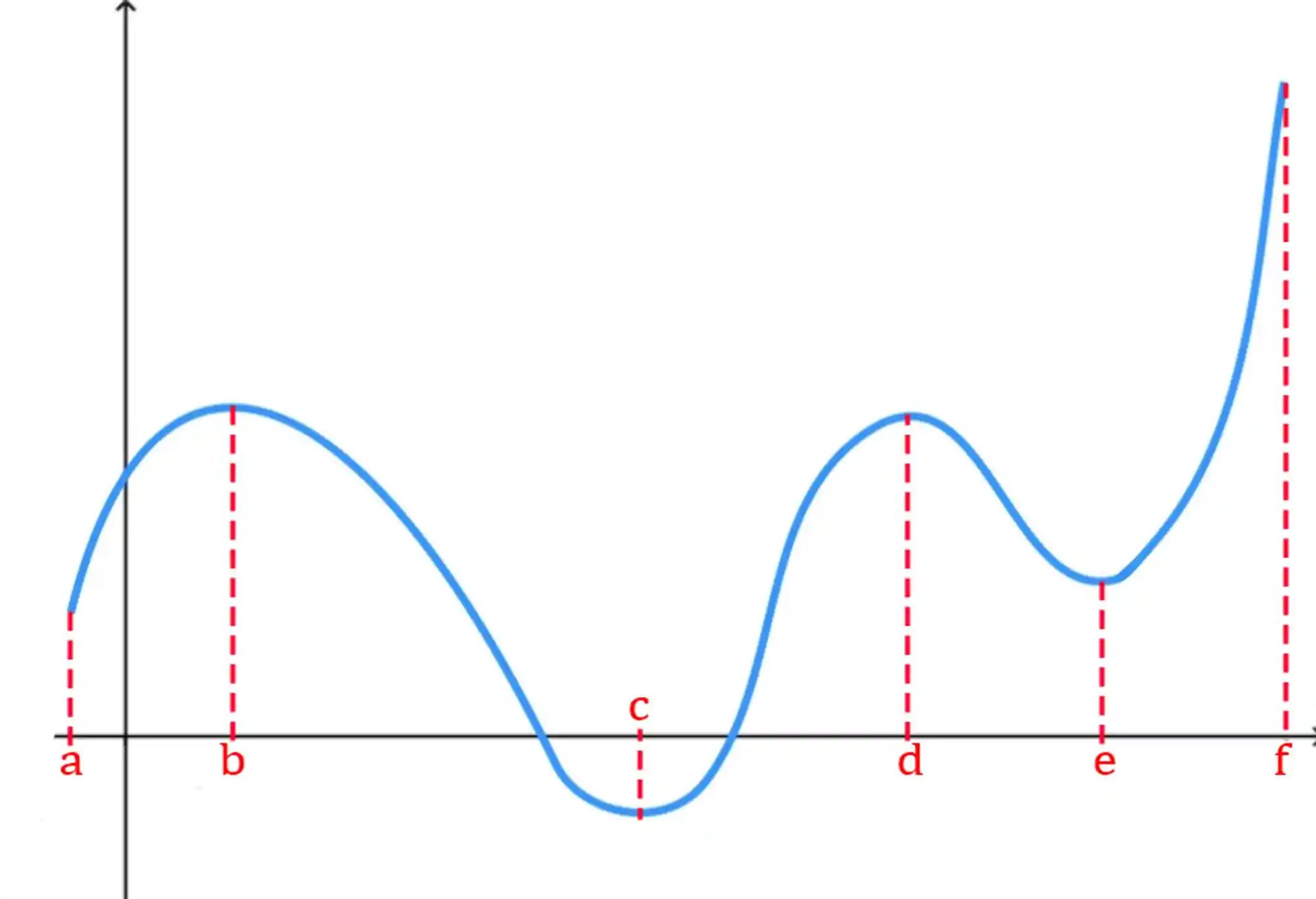
Gráfico com pontos críticos.
Gráfico com pontos críticos.

Agora eu te pergunto: quais são os pontos máximos e mínimos dessa função?

Ué, o ponto tem o maior valor e o tem o menor. Então é o ponto máximo e é o ponto mínimo, não é?

Parcialmente correto, sabe por quê? Aqueles outros pontos marcados ali também têm uma certa relevância pra gente.

Apesar de eles não serem os máximos ou mínimos absolutos, na região ali perto de cada um eles também são os maiores ou menores! Por isso, damos a eles os nomes de máximos ou mínimos locais.

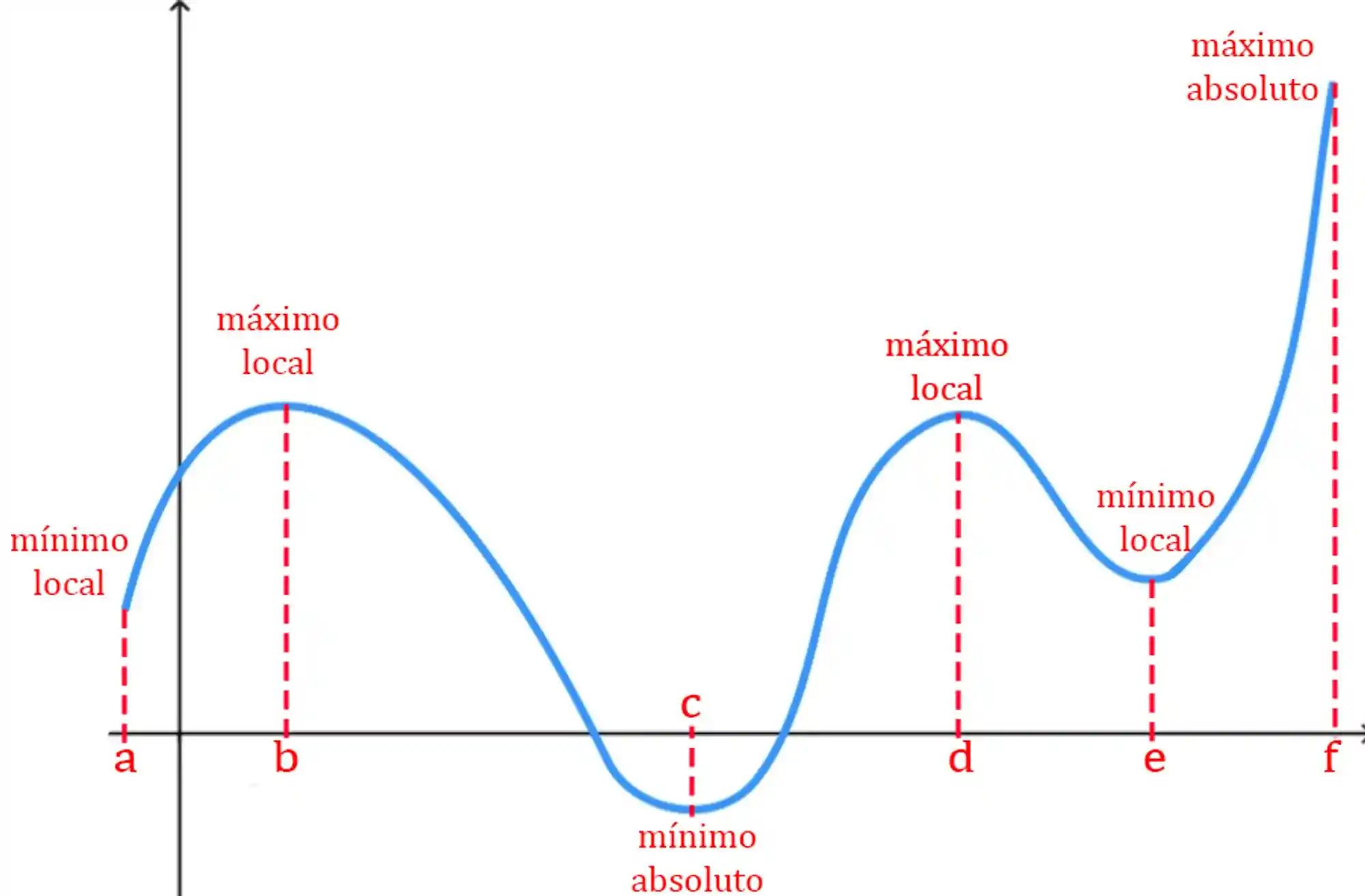
Máximos e mínimos locais e absolutos de um gráfico.
Máximos e mínimos locais e absolutos de um gráfico.

Então, para termos certeza que é mínimo global, ou absoluto, temos que comparar com os outros pontos que encontrarmos. Ele só será mínimo absoluto se:

$$f(c)

E não só isso! Também temos que garantir que a função não dispara pra cima ou pra baixo em algum momento fora do intervalo que desenhamos aqui! Afinal, se a função for contínua em todos os reais, não conseguimos desenhar todo o gráfico, né?

E como fazemos isso aí? Com o limite da função com tendendo a infinito negativo e infinito positivo!

Isso vai nos mostrar se todos os valores possíveis de são maiores que nosso ponto 😄

Se liga no resuminho pra saber se um ponto de máximo ou mínimo é global:

Resumo: pontos de máximo e mínimo absolutos.
Resumo: pontos de máximo e mínimo absolutos.

Como encontrar os pontos máximos e mínimos de uma função?

Beleza, olhando pro gráfico assim é fácil, mas eu preciso ficar desenhando gráfico pra toda função?

Ainda bem que não! Os pontos críticos de uma função são aqueles em que a derivada vale zero. Então, a gente pode encontrar os pontos críticos de uma função tomando a primeira derivada e igualando a zero.

Pra te mostrar porque isso ocorre, olha só pra esse gráfico da função :

Gráfico da função
Gráfico da função

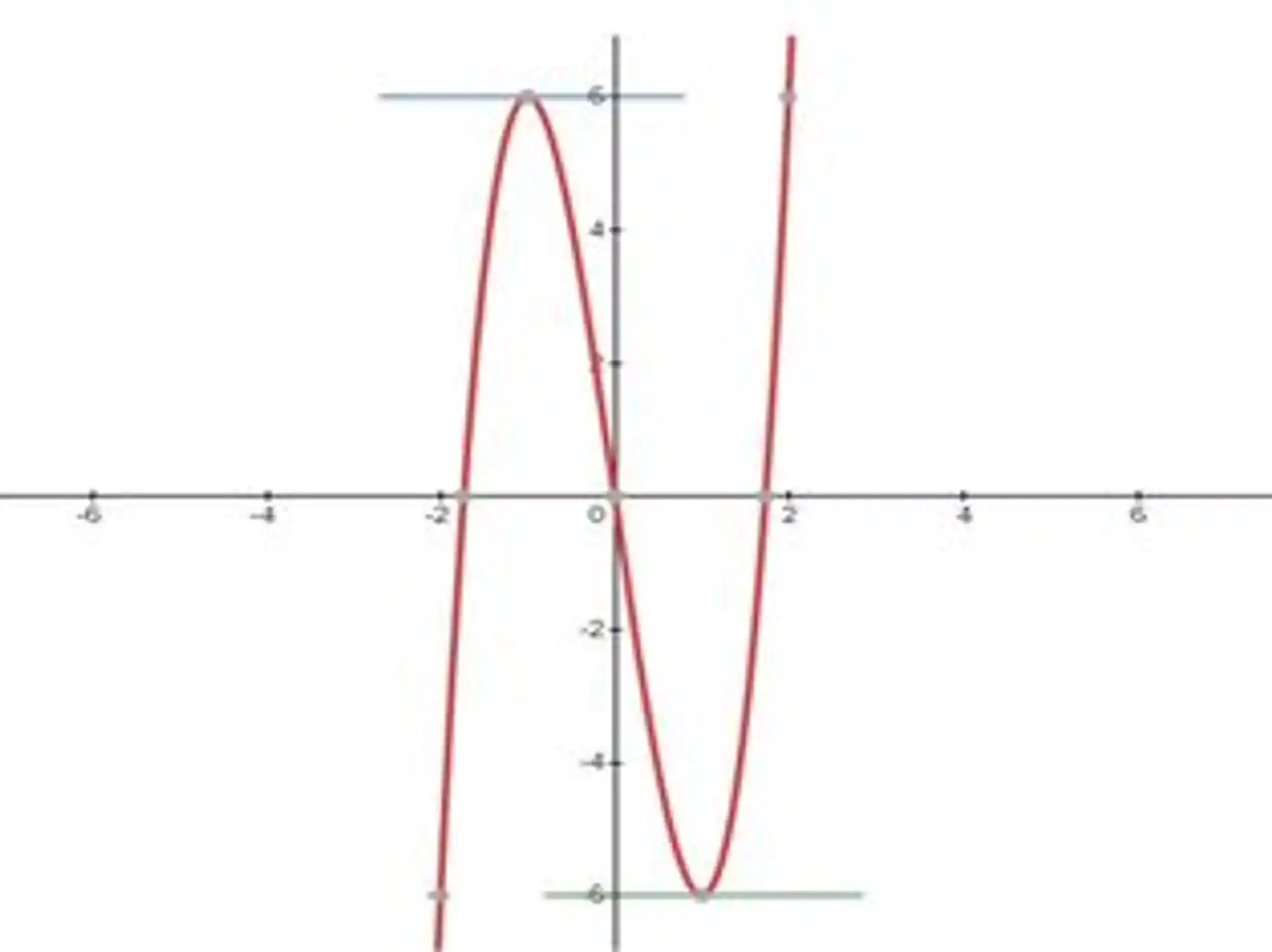
Consegue perceber que para os pontos de máximo e de mínimo a reta tangente ao gráfico é horizontal? Isso quer dizer que o coeficiente angular delas é zero!

Tá… E daí?!

Lembra que o coeficiente angular da reta tangente a um ponto é exatamente a derivada da curva naquele ponto? Então, isso quer dizer que a derivada da curva vai ser nula nesses pontos!

Bora ver quais são esses pontos pra função que a gente colocou ali em cima?

Vamos derivar isso aí.

E se igualarmos a zero:

Então teremos os pontos críticos em e 😄

Teste da primeira derivada

Beleza, já sabemos encontrar os pontos críticos. Mas agora, como saber se os pontos encontrados são de máximo ou de mínimo?

Para pontos de máximo, a derivada de valores à esquerda é positiva e a derivada de valores à direita é negativa.

Pensa no seguinte: para obter um ponto de máximo, a função tem que crescer (reta tangente crescente e derivada positiva), chegar num ponto máximo (derivada nula) e então começar a decrescer (derivada negativa)!

E o exato oposto vale para os pontos de mínimo! A derivada de valores à esquerda é negativa e a derivada de valores à direita é positiva.

Só pra garantir seu entendimento, vamos resolver juntos esse exemplo 👇

EXEMPLO: Encontre os pontos críticos da função e indique se são de máximo ou de mínimo.

Bora começar fazendo a derivada disso aí:

E igualar a zero:

Nossa função só tem um ponto crítico, que é o .

Pra saber se ele é de máximo ou de mínimo, vamos descobrir os sinais das derivadas à direita e à esquerda dele. Pode pegar qualquer valor, desde que você tenha certeza que a função não passe por nenhum outro ponto crítico antes de chegar no valor que você escolheu!

Eu vou escolher e . Então é só jogar esses valores na equação da derivada que encontramos ali em cima.

Então, a derivada à direita de é positiva e à esquerda é negativa!

Qual o raciocínio aqui? A função vai decrescendo (com uma tangente negativa) chega num ponto e começa a crescer (com tangente positiva). Esse ponto é de máximo ou de mínimo?

Só pode ser de mínimo!

Maravilha! Então já aprendemos a encontrar os pontos críticos de uma função e como determinar se são mínimo ou máximo por meio do teste da primeira derivada.

Quer mais exercício? Se liga nesse vídeo com um resolvido passo a passo 👇

Teste da segunda derivada

O teste da segunda derivada permite que você determine se um ponto crítico é máximo ou mínimo a partir da concavidade da função naquele ponto.

Lembra que a concavidade de uma função é dada pelo sinal da segunda derivada? Então, se a gente for pensar bem, a concavidade da função aponta para baixo em pontos de máximo e para cima em pontos de mínimo.

Podemos juntar essas duas informações e chegar nesse postulado aqui:

Teste da segunda derivada.
Teste da segunda derivada.

Resumo

Bora compilar tudo o que aprendemos?

  1. Encontramos os pontos críticos de uma função fazendo a primeira derivada igual a zero.
  2. Pelo teste da primeira derivada: se a derivada de um ponto próximo ao ponto crítico pela esquerda for positiva e a derivada de um ponto próximo ao ponto crítico pela direita for negativa, o ponto crítico é de máximo. Caso contrário, ele é de mínimo.
    Resumo: teste da primeira derivada.
    Resumo: teste da primeira derivada.

  1. Pelo teste da segunda derivada: se a segunda derivada for negativa, o ponto crítico é de máximo, caso contrário, ele é de mínimo.
  2. Se o ponto crítico for de máximo, ele será máximo global se for maior que todos os outros pontos .

Como encontrar os pontos máximos e mínimos de uma função?

Resumo

Exercícios Resolvidos

Exercício Resolvido #1

George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 299-1. MODIFICADO

Identifique os pontos de máximo e mínimo e de inflexão da função abaixo.

y = x 3 3 - x 2 2 - 2 x + 1 3

Passo 1

Os pontos de máximo e mínimo são pontos críticos. Para encontrá-los, vamos primeiro derivar a função:

y ' = x ² - x - 2

Passo 2

Os pontos críticos estão localizados onde a derivada não existe ou é zero. Essa derivada é um polinômio, então vai sempre existir. Vamos ver quando ela será zero:

x ² - x - 2 = 0

Por Bhaskara:

x 1 = - b + b 2 - 4 a c 2 a = 1 + 1 - 4 ⋅ 1 ⋅ ( - 2 ) 2 ⋅ 1 = 1 + 1 + 8 2 = 1 + 3 2 = 2

Da mesma maneira:

x 2 = 1 - 3 2 = - 1

Esses serão os pontos críticos da função. Antes de determinar se são pontos de máximo ou mínimo, vamos calcular os pontos de inflexão.

Passo 3

Os pontos de inflexão ocorrem quando a segunda derivada não existe ou é zero. Para isso, derivamos a função novamente:

y ' ' = 2 x - 1

Por se tratar de um polinômio, a segunda derivada sempre existirá. Será zero quando:

2 x - 1 = 0 ⟹ x = 1 2

Este será nosso ponto de inflexão.

Passo 4

Voltamos agora aos pontos críticos para determinar qual é máximo e qual é mínimo. Cara, por que você deu volta e não seguiu com isso antes? Porque, ao calcular os pontos de inflexão, nós calculamos a segunda derivada da função. E com a segunda derivada fica muito mais fácil encontrar os pontos de máximo e mínimo.

Só precisamos aplicar o teste da segunda derivada. Nos pontos críticos:

f ' ' x 1 = f ' ' 2 = 2 ⋅ 2 - 1 = 3 > 0

Como a segunda derivada é positiva, trata-se de um ponto de mínimo.

Para o segundo ponto crítico:

f ' ' x 2 = f ' ' - 1 = 2 ⋅ - 1 - 1 = - 3 < 0

Como a segunda derivada é negativa, trata-se de um ponto de máximo.

Toda vez que a gente quer encontrar um ponto de máximo ou mínimo, você deve optar em aplicar o teste da segunda ou da primeira derivada. Quando a segunda derivada é fácil de calcular, foi dada, ou você já vai ter que calculá-la de qualquer forma, opte pelo teste da segunda derivada, que é mais rápido.

Se fossemos aplicar o teste da primeira derivada aqui. Deveríamos escolher um ponto a esquerda e direita do ponto crítico, sem nunca extrapolar um ponto crítico que não é o que gente está tratando.

Para x 1 = 2 . Podemos escolher x = 0 e x = 3 :

f ' 0 = 0 - 0 - 2 < 0 ; f ' 3 = 3 2 - 3 - 2 = 9 - 3 - 2 = 4 > 0

Como é negativo à esquerda e positivo à direita, temos, como antes, um ponto de mínimo.

Para x 2 = - 1 . Podemos escolher x = - 2 e x = 0

f ' - 2 = - 2 2 + 2 - 2 = 4 > 0 ; f ' 0 < 0

Como é positivo à esquerda e negativo à direita, temos, como antes, um ponto de máximo, como no gráfico:

Resposta

Mínimo: x = 2 ; Máximo: x = - 1 . Inflexão: x = 1 / 2 .

Exercício Resolvido #2

UFRJ - Cálculo 1 - PF 2015.1 – 3

Considere o polinômio y = A x 3 + 6 x 2 - B x , onde A e B são constantes reais. É possível determinar valores para A e B tais que o gráfico de y tem um ponto de máximo local quando x = - 1 e um ponto de inflexão quando x = 1 ?

Passo 1

O que significa matematicamente para um gráfico de polinômio ter um máximo local? E um ponto de inflexão? Lembra, os máximos locais são pontos onde a derivada muda de sinal, o que significa que neles a derivada é nula ou não existe no ponto. Nos pontos de inflexão quem é nula ou não existe é a derivada segunda.

Basicamente, o que a questão nos fala é que ela quer:

y ' - 1 = 0

y ' ' 1 = 0

Passo 2

E como é a equação de y ' e de y ' ' ? Vamos derivar para descobrir!

y ' x = A x 3 ' + 6 x 2 ' - B x '

= 3 A x 2 + 12 x - B

y ' ' x = 3 A x 2 ' + 12 x ' - B '

= 6 A x + 12

Passo 3

Substituindo os pontos que a questão falou:

y ' - 1 = 3 A - 1 2 + 12 - 1 - B = 0

3 A - B = 12

y ' ' 1 = 6 A 1 + 12 = 0

6 A = - 12

Agora basta resolver o sistema que esses caras geraram:

3 A - B = 12 6 A = - 12

A = - 2     ;     B = - 18

Passo 4

Se x = - 1 for um máximo, a derivada é positiva antes e negativa depois. Sendo assim, vamos descobrir os pontos em que a derivada é nula!

y = - 2 x 3 + 6 x 2 + 18 x

y ' = - 6 x 2 + 12 x + 18

Como y ' nada mais é do que uma função do 2º grau, nós podemos utilizar a fórmula de Bhaskara para calcularmos suas raízes. Começando pelo ∆ , temos:

∆ = b 2 - 4 * a * c

∆ = 144 - 4 ( - 6 ) ( 18 )

∆ = 144 + 432

∆ = 576

Aplicando o valor que descobrimos para ∆ na segunda parte da fórmula:

x = - b ± ∆ 2 a

x = - 12 ± 24 - 12

x = 1 ± 2

Como a concavidade é para baixo, a derivada será positiva entre -1 e 3 e negativa para x < - 1 e x > 3 . Então, x = - 1 é um ponto de mínimo!

Resposta

Portanto, não é possível.

Exercício Resolvido #3

George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education Ltda, 2009, pp. 291-21. MODIFICADO

Sendo:

g x = x 8 - x ²

a ) Encontre os intervalos onde a função é crescente e decrescente.

b ) Em seguida, identifique os valores extremos locais da função, se houve, informando onde ela os assume.

c ) Alguns desses valores extremos são absolutos? Quais?

Passo 1

a ) Para encontrar onde a função cresce ou decresce, devemos encontrar as raízes da derivada ou determinar quando ela não existe e testar valores à esquerda e à direita desses pontos. Resumindo, aplicamos o teste CD.

Para tal, vamos derivar. Usando a regra do produto: g ' x = 8 - x 2 + x ⋅ - 2 x 2 8 - x 2 = 8 - x 2 - x 2 8 - x 2 = 8 - x 2 - x ² 8 - x 2

g ' x = 8 - 2 x 2 8 - x 2

Passo 2

As raízes vão ser determinadas pelos numeradores:

8 - 2 x 2 = 0 ⟹ x 2 = 4 ⟹ x = ± 2

E não vai existir para quando:

8 - x 2 = 0 ⟹ x = ± 2 2

Passo 3

Agora, vamos testar valores à esquerda e à direita:

Para x = - 2 , podemos escolher x = - 5 / 2 e x = 0 :

f ' - 5 / 2 = 8 - 2 - 5 / 2 2   8 - - 5 / 2 2 = 8 - 25 / 2 8 - 25 / 4 = - 9 / 2 ( 32 - 25 ) / 4 < 0

f ' 0 = 8 - 0 8 - 0   > 0

Então a derivada é negativa à esquerda e positiva à direta de x = - 2 .

Para x = 2 , podemos escolher x = 0 e x = 5 / 2 :

f ' ( 0 ) > 0

f ' 5 / 2 = 8 - 2 5 / 2 2   8 - 5 / 2 2 < 0

Então a derivada é positiva à esquerda e negativa à direta de x = 2 .

Para x = - 2 2 , não há valores à esquerda, pois a derivada terá raiz negativa no denominador. Para valores à esquerda, já sabemos, pois:

f ' - 5 / 2 < 0

Para x = 2 2 , não há também valores à direita, pelo mesmo motivo de cima. Para valores à esquerda, sabemos que:

f ' 5 / 2 < 0

Com todas essas informações. Temos que:

Função crescente para x ∈ ( - 2 ,   2 ) .

Função decrescente para x ∈ - 2 2 , - 2 ∪ ( 2,2 2 ) .

Passo 4

b ) Para acharmos máximos e mínimos, determinamos os pontos críticos que serão as raízes da derivada ou quando ela não existe. Já determinamos isso aí. Serão os pontos:

x = - 2 ; x = 2 ; x = 2 2 ; x = - 2 2

Já também testamos os sinais à esquerda e à direita de cada ponto, que é o teste da primeira derivada.

A derivada é negativa à esquerda e positiva à direta de x = - 2 . Então temos um ponto de mínimo aqui.

A derivada é positiva à esquerda e negativa à direta de x = 2 . Então temos um ponto de máximo aqui.

A derivada é negativa à direta de x = - 2 2 e não existe à esquerda

A derivada é negativa à esquerda de x = 2 2 e não existe à direita.

Vai ficar assim:

Passo 5

c ) Agora precisamos saber se são extremos locais ou absolutos. O ponto de máximo é:

x = 2  

Para x = 2 :

f 2 = 2 8 - 2 2 = 2 4 = 4

Para as fronteiras da função:

x = - 2 2 :

f - 2 2 = - 2 2 8 - - 2 2 2 = 0

x = 2 2 :

f 2 2 = 2 2 8 - 2 2 2 = 0

O ponto x = 2 é um ponto de máximo que é maior que os valores na fronteira. Então é um ponto de máximo global.

Se houvesse outros pontos de máximo, x = 2 também deveria ser maior que estes para ser máximo global.

Para o ponto de mínimo:

Para x = - 2 :

f - 2 = - 2 8 - - 2 2 = - 2 4 = - 4

O ponto x = - 2 é um ponto de mínimo que é menor que os valores na fronteira. Então é um ponto de mínimo global.

Se houvesse outros pontos de mínimo, x = - 2 também deveria ser menor que estes para ser mínimo global.

Resposta

a ) Função crescente para x ∈ ( - 2 ,   2 ) .

Função decrescente para x ∈ - 2 2 , - 2 ∪ ( 2,2 2 ) .

b ) A derivada é negativa à esquerda e positiva à direta de x = - 2 . Então temos um ponto de mínimo aqui.

A derivada é positiva à esquerda e negativa à direta de x = 2 . Então temos um ponto de máximo aqui.

c ) x = 2 é ponto de máximo global. x = - 2 é mínimo global.

Exercício Resolvido #4

UFF - Cálculo IA - P2 Sérgio Almaraz 2014.2 - 3ª

  1. Mostre que a função

f x = ln ⁡ x x

Possui um máximo absoluto em x = e

Passo 1

Para ser máximo, o ponto deve ser crítico e a derivada tem que ser positiva à sua esquerda e negativa à sua direita. Para verificar isso, vamos derivar:

f ' x = x ln ⁡ x ' - [ x ] ' ln ⁡ ( x ) x ² = 1 - ln ⁡ ( x ) x 2

Passo 2

Verificamos se x = e é ponto crítico:

f ' e = 1 - ln ⁡ e x 2 =   0

A esquerda de x = e , temos e 1 / 2 :

f ' e 1 / 2 = 1 - ln ⁡ ( e 1 / 2 ) e = 1 - 1 / 2 e > 0

A direita de x = e , temos e 2 :

f ' e 2 = 1 - ln ⁡ ( e 2 ) e 4 = 1 - 2 e 4 < 0

É um ponto de máximo. Precisamos saber se é global.

Passo 3

Vai ser máximo global se for maior que outros pontos de máximo e maior que as fronteiras.

Não há outros pontos de máximo, pois, além de x = e , só x = 0 é ponto crítico. E não valores menores que x = 0 para testar, uma vez que não fazem parte do domínio (ln de valores negativos).

Temos que testar as fronteiras.

lim x → 0 ⁡ ln ⁡ ( x ) x ⟹ - ∞ 0 ⟹ - ∞

E:

lim x → ∞ ⁡ ln ⁡ ( x ) x ⟹ ∞ ∞

Podemos aplicar L’Hôpital:

lim x → ∞ ⁡ ln ⁡ ( x ) x = lim x → ∞ ⁡ ln ⁡ ( x ) ' [ x ] ' = lim x → ∞ ⁡ 1 / x 1 = 0

Assim, não existem valores maiores que:

f e = ln ⁡ ( e ) e = 1 e

Esse é, portanto, um ponto de máximo global ou absoluto.

Resposta

Como queríamos demonstrar.

Exercício Resolvido #5

George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 291-40. MODIFICADO

Se:

k x = x 3 + 3 x 2 + 3 x + 1 ,   - ∞ < x ≤ 0

a ) Identifique os valores extremos locais da função nos domínios dados e informe onde ela os assume.

b ) Alguns desses valores extremos são absolutos? Quais?

Passo 1

Para determinar os pontos de máximo e mínimo, calculamos os pontos críticos, derivando:

k ' x = 3 x 2 + 6 x + 3 ,   - ∞ < x ≤ 0

Os pontos críticos estão localizados onde a derivada não existe ou é zero. Sempre vai existir pois é um polinômio. Será zero quando:

3 x 2 + 6 x + 3 = 0

Que tem raiz x = - 1 .

Passo 2

Vamos escolher valores à esquerda e à direita para aplicar o teste da primeira derivada.

Em x = - 1 , podemos escolher x = - 2 e x = 0 :

k ' - 2 = 3 - 2 2 + 6 - 2 + 3 = 12 - 12 + 3 > 0

k ' 0 = 0 + 0 + 3 > 0

A derivada é positiva a esquerda e a direita, então não é ponto de mínimo nem de máximo.

Passo 3

b ) Não há nada concluir.

Resposta

a ) Nem máximo, nem mínimo.

b ) Não há nada concluir.

Exercícios de Livros Relacionados

O gráfico da derivada f ' de uma função f está mostrado. (a) Em quais intervalos f é crescente ou decrescente? (b) Em que valores de x a função f tem um mínimo ou máximo local?
Encontre os números críticos da funçãof (x) = 5 x^2 + 4 x
Encontre os valores de máximo e mínimo absoluto de f no intervalo dado f x = 3 x 2 - 12 x + 5 ,[ 0,3 ]
É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem? f ' x = 100 cos 2 ⁡ x 10 + x 2 - 1
Encontre os números críticos da funçãoh (p) = (p - 1)/(p^2 + 4)