É dada uma fórmula para a derivada de uma função. Quantos números críticos ela tem?
Passo 1
Opa! O enunciado nos da a seguinte derivada:
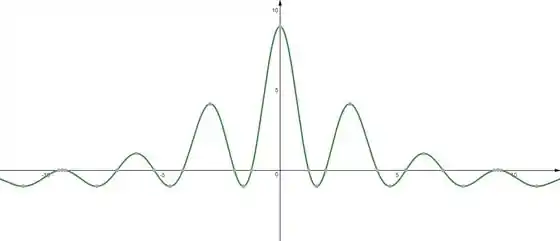
O número crítico de uma função é encontrado derivando uma função e igualando ela a zero. Como já temos a derivada e essa função é um cado complicada, vamos usar seu gráfico:
Passo 2
Ao analisarmos o gráfico da função vemos que a medida que vamos pra valores de maiores, tanto do lado positivo quanto o lado negativo, o gráfico não toca o eixo . Então tudo o que temos que fazer é contar os pontos onde mostrados no gráfico!
Assim possui 14 raízes, ou seja, corta o eixo 14 vezes, logo, possui 14 números críticos
Resposta
possui 14 números críticos